AERO2463 Computational Engineering Analysis Assignment 4

School of Engineering

Computational Engineering Analysis AERO2463

Assignment 4

4.1 Curve Fitting - Polynomial Fitting of Data

4.2 Finite Differences and Differential Equations

School of Engineering

Computational Engineering Analysis - AERO2463

Assignment 4.1

Curve Fitting - Polynomial Fitting of Data

Assessment:

The MATLAB Assignment 4.1 is worth 5%.

Objectives:

Generate curves by fitting data using polynomials

Submission Instructions:

There are two m-files provided to you on Canvas. One is the template for the function file you are to submit and the other is a script file that you should use to test your function file (please do not submit the script file used for testing your function).
Submit a single function m-file via Canvas before submission due date specified above.
Note that the Last Name and Student ID are required as a comment line at the beginning of the m-file, but after the function header.
The m-file submitted on Canvas should be named as:

o LastName_StudentID_polynomial_fitting.m (write your function in this one)

Do not zip any files.
Failure to submit before the deadline will require a reasonable explanation and approval from the Course Coordinator before any later submission can be accepted.
RMIT late assignment submission policy will apply (10% deduction of marks for each day delay).
Use the Special Consideration process for any submission later than one week.
Submit only the files related to the Assignment 4.1.

Background

When dealing with data from experiments or computations, the data will be discrete and not have uniform spacing. Fitting the data within a polynomial can help to predict outputs and to deal with the data in further calculations.

The aim of fitting your discrete data to a polynomial is to be able to predict a value of the dependent variable in terms of the independent variable for those values which do not have corresponding discrete data. Depending on the relationship of the variables, polynomials of different orders should be used to find a good fit between the polynomial and the real data. In the figure shown below, real measurements of liquid water density were taken in increments of 10 °C and several polynomials were calculated using polyfit()to see the correlation between them and the discrete data.

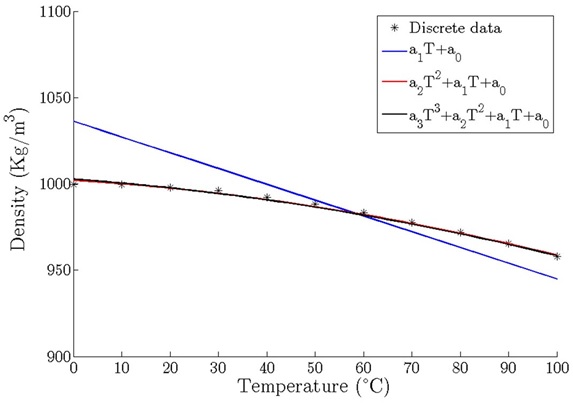
After a polynomial is obtained, we can try to interpolate or extrapolate y-values for any x-value. Be careful if you are extrapolating outside the boundaries of your discrete data, the polynomial could fit well inside your data, but maybe it does not represent well the reality outside them. What is the density of liquid water (pressurized) for temperatures greater that 100°C? In the figure above, we can try to extrapolate them, but we do not know if the physical phenomena will be still fitting our polynomials.

Task

Your task is to write a function which takes two vectors, x (independent variable) and y (dependent variable), and fits polynomials from order 1 (linear relation) up to order 10 (or the maximum order possible for the data size). The function should plot the x and y data with markers (no line) and plot each fitted polynomial (with lines), all on the same plot axis. In a separate figure (or in separate plots within one figure using subplot), plot the interpolated/extrapolated y value for a given x-point defined by the user.

Coding Requirements

Use the MATLAB built-in function polyfit.
You should not make any sub-functions inside the function.
Ensure the x and y data given to the function have the same length. If it is not the case, the function MUST use the error() function to give the user an error message and exit.
There must NOT be any user interaction within the function.
To fit a function with a polynomial of an order (also called grade or degree) “n” there must be at least “n+1” points. Your code MUST detect if the number of points is not sufficient enough and show an error message before trying to calculate wrong polynomials.
The user will enter the x and y vectors to the function from the script, and it will also specify a point “x2” which the function will use to extrapolate its value y(x2) using all the polynomials calculated.
You should create extra x-points in your function to make the polynomial line plots smoother using more points.
If the given data fits exactly a polynomial of an order lower than 10, your function MUST NOT plot the polynomials of a greater order. You could use a tolerance to test this.

Hint: In order to fulfill requirement number 8, you should compare your coefficients with a certain tolerance (e.g 10e-6) if you calculate your polynomial, and from certain coefficient all the higher order coefficients (beyond it) are lower than the tolerance, you may assume that it is a perfect fit for a polynomial, excluding those higher order coefficients (i.e. they are equal to zero).

Examples

Example 1

In this first example, the data fits exactly an order 2 polynomial, therefore the code will only plot two polynomials (order 1 and 2)

The user will produce a call to the function in the workplace such as:

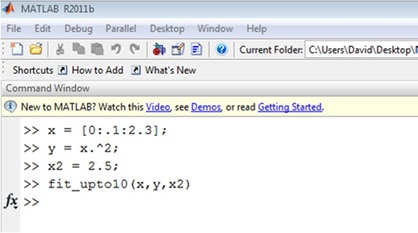
In this case, the function output will produce two plots. The first one is the polynomial fits with the original data. As the polynomial of order 2 fits exactly the function, only 2 polynomials have to be plotted.

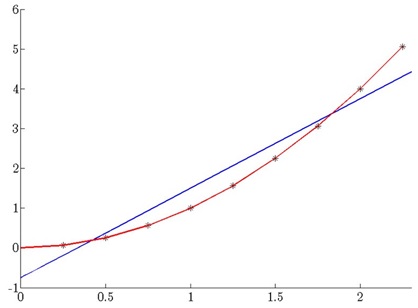
The second plot output contains the predictions at position x2 (x-axis is polynomial order, y-axis is the predicted y value). You have to plot only the number of predictions of the plotted polynomials. As in this case the original data was a perfect x^2 relation, we expect all polynomials of this order or greater to perfectly fit the data and extrapolate the same value. In this subplot you can choose between plotting the guesses of all the polynomials or plot only those guesses for the polynomials shown in the previous figure.

Example 2.

In this case, the fitting will not be perfect with any polynomial, and the code will have to plot all the required polynomials:

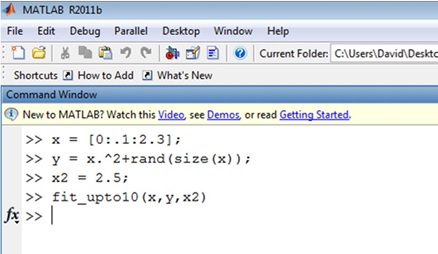
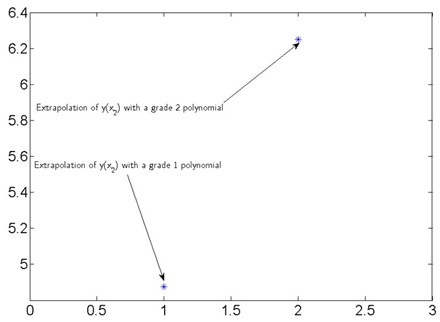
The two plots produced will look like the ones below:

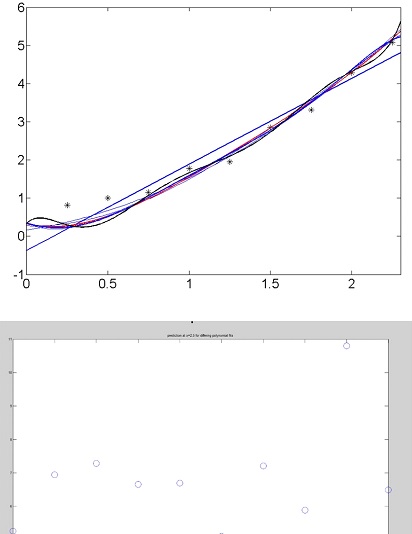
The small amount of scatter in the data leads to dramatically different predictions of the data at an x value of 2.5 (the last known data point was 2.3).

The lesson to be learnt here is: Never extrapolate data with a polynomial unless you know the data is governed by a polynomial of a given order.

When creating software it is very important to ensure your program satisfies the requirements.

Requirements are often very specific as your software may need to interact with user and/or other software components in a very specific way.

Please heed the following warning and ensure your program meets all the requirements described herein before submitting it.

Assessment

Correctly plots fitted polynomials as specified 60%

Correctly plots interpolated/extrapolated y-value for user input x-value in separate plots 20%

If data set mathches a polynomial, higher-order polynomials are not fitted or plotted 20%

Code does not produce error message if x and y are of different size. -20%

Code does not produce error message applied to data set with less than 11 points. -20%

Appropriate deductions for not meeting requirements (e.g. wrong file name) -20%

IMPORTANT: HINTS (DOs and DON’Ts)

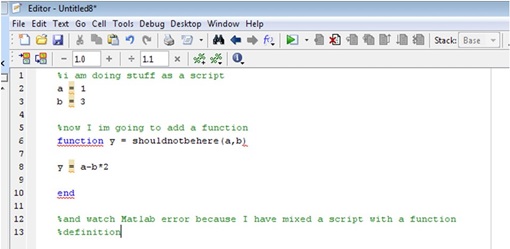
DO NOT PLACE CODE ABOVE YOUR FUNCTION DEFINITION. This is mixing a script and function and cannot be done. The user will pass the data they wish to use to the function via the input arguments!

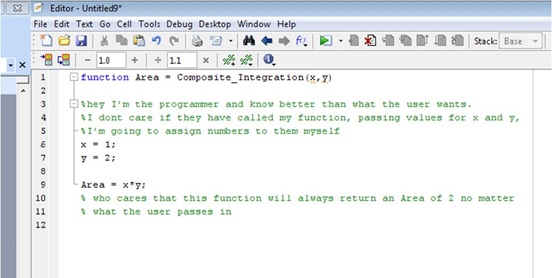
DO NOT STORE SOMETHING TO X, X2 OR Y IN YOUR FUNCTION. If you store values in x, x2 or y in your function, then it will overwrite what the user specified for x, x2 and y.

TEST YOUR CODE: Your code may fit well a provided set of data (but it may not fit for another data set). Make up your own data (that you know the answer to) and test that your function returns the correct results.

TUTORIALS: Please do the learning exercises in the tutorials. They will teach you the skills necessary to do this task.

School of Engineering

Computational Engineering Analysis - AERO2463

Assignment 4.2

Finite Differences and Differential Equations

Assessment:

The MATLAB Assignment 4.2 is worth 5%.

Objectives:

Solve a mechanics problem to calculate the displacement, strain and stress in a 1D elastic structure using the Finite Difference Method.

Submission Instructions:

You should submit ONE function m-file.
In the m-file code, you MUST write your name and student ID as a comment line in the mfile.
Use the templates provided on Canvas.

The m-file should be named as: Last Name_Student ID_FiniteDifference.m (write your function in here)

Please note: You will have to include the same function name as the above file name inside your function file to run it.

Do not zip the file.
Failure to submit the assessment solution file through Canvas before the end of submission date and time will need special consideration approval from the coordinator to re-submit (with reasonable explanation).
In that case, RMIT policy of late assignment submission will apply (10% deduction of marks for each day delay).
Another m-file calledm is provided to try and call your function. Do NOT submit this file.

AERO2463 Computational Engineering Analysis: Assignment 4, 2018

Problem:

Consider the example of a compression or tensile mechanical test. A sample one-dimensional rod or beam type structure is placed in the tensile test machine. One end is fixed whereas the other end is subject to an imposed displacement. This displacement generates strains and stresses in the structure.

We consider the 1D configuration described by the figure below:

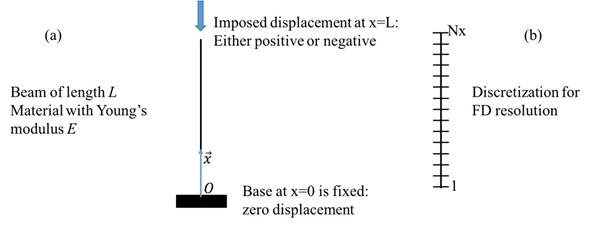
We consider a static problem, where a specific displacement is imposed on a simple 1D rod structure. One end of the rod is fixed (zero displacement) at x=0, and a displacement of value D is imposed at the other end at x=L.

Objective: The aim is to determine the displacement field in the structure for a given displacement at the end point, as well as the strain and stress field, using a second order Finite Differences (FD) method.

The strain ( ) relation is given by the following equation for the current 1D problem:

The stress is then computed as:

where E is the Young’s modulus.

The 1D equation of equilibrium in the absence of an external force is given by. 0

which in 1D corresponds to

This last equation needs to be solved with the Finite Differences method. The structure of length L will be discretized (divided) into N_x elements (segments), as shown in the figure above. Here are some hints describing the intermediate steps required to solve this problem numerically.

AERO2463 Computational Engineering Analysis: Assignment 4, 2018

Using the expansion in Taylor series, write the central difference scheme for the second order partial derivative ⁄ . This will be true for interior nodes 2 to N_x-1. Special care must be taken for the first and last nodes.
For the first node (x=0) the displacement is labeled . The value of this displacement is known since it is a boundary condition, 0. We account for the first term as follows:

1 0

For the last node, (x=L) the displacement is labeled . This displacement is also known because it is the second boundary condition: . Similarly, we account for the last term as follow:

You now have a general scheme for node ∈ 2, 1 , and a simple relation for the first node 1, and the last node . That is all you need to construct a linear system, where U is the unknown vector of displacement to be computed, is a square matrix defined from the FD scheme above, and B is a vector containing the imposed displacement.

Construct a square matrix of dimension N_x× N_x to write the linear system .

Then, you can start programming in MATLAB.

In your MATLAB function Last Name_Student ID_FiniteDifference.m, you need to:
1. Discretize the geometry (divide L in N_x-1 segments or cells, to have N_x nodes).
2. Construct the matrix (start with a zeros (of size N_x) matrix and use a for loop to modify the non-zero terms). First and last columns need to be defined separately to incorporate boundary conditions.
3. Construct a vector B to store the imposed displacement.
4. Solve the problem to obtain the displacement U by inverting the linear system. Plot the displacement field along the structure.
5. Compute the strain from the displacement. Plot the strain along the structure.
6. Compute the stress and plot it along the structure. What do you observe and conclude?

Your function must produce 3 plots (displacement, strain and stress along the length of the rod structure) and return 2 vectors X and U, respectively, for the discretized domain and the displacement. Since the strain and stress are calcualted for each 1D segment (element), these can be plotted against the displacement at the upper node for that corresponding segment.

Assessment Criteria

Correct implementation of the FD scheme for displacement 60%
Correct computation of strains and stresses 20%
Correct plotting 20%
Renaming function, inputs or outputs -25%
Using a built-in ODE solver -25%

Australia Universities

ACT

Australian Catholic University

Australian National University

Bond University

Central Queensland University

Charles Darwin University

Charles Sturt University

Curtin University of Technology

Deakin University

Edith Cowan University

Flinders University

Griffith University

Holmes Institute

James Cook University

La Trobe University

Macquarie University

Monash University

Murdoch University

Queensland University of Technology

RMIT University

Southern Cross University

Swinburne University of Technology

University of Adelaide

University of Ballarat

University of Canberra

University of Melbourne

University of Newcastle

University of New England

University of New South Wales

University of Notre Dame Australia

University of Queensland

University of South Australia

University of Southern Queensland

University of Sydney

University of Tasmania

University of Technology Sydney

University of the Sunshine Coast

University of Western Australia

University of Wollongong

Victoria University

Western Sydney University

Year 11 - 12 Certification Assignment

Australian Capital Territory Year 12 Certificate

HSC - Higher School Certificate

NTCE - Northern Territory Certificate of Education

QCE - Queensland Certificate of Education

SACE - South Australian Certificate of Education

TCE - Tasmanian Certificate of Education

VCE - Victorian Certificate of Education

WACE - Western Australia Certificate of Education

AERO2463 Computational Engineering Analysis Assignment 4

Diploma Universities Assignments