HOME

Multiple Regression Analysis: Estimation and Inference

The business problem facing the director of broadcasting operations for a television station was the issue of standby hours (i.e. hours in which unionized graphic artists at the station are paid but are not actually involved in any activity) and what factors were related to standby hours. The study included the following variables:

Standby hours (Y)—total number of standby hours in a week

Total staff present (X¹)—Weekly total of people-days

Remote hours (X²)—Total number of hours worked by employees at locations away from the central plant

Data were collected for 26 weeks; these data are organized and stored in Standby.

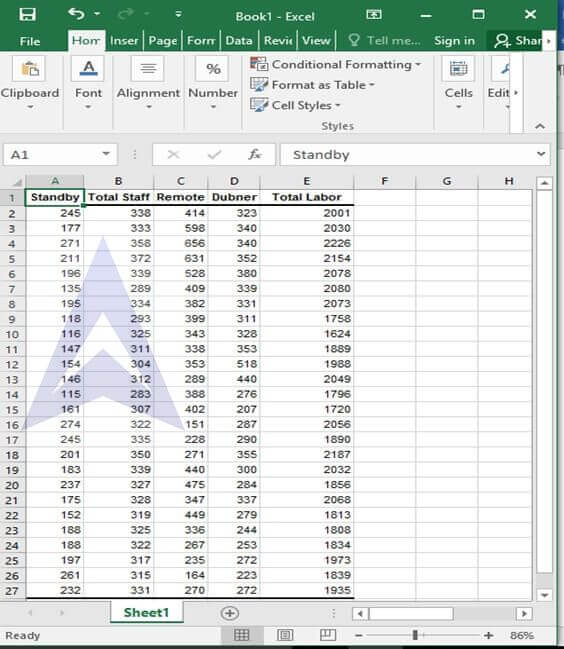
Step 1

Copy data on to an excel sheet.

Standby Total Staff Remote Dubner Total Labor
245 338 414 323 2001
177 333 598 340 2030
271 358 656 340 2226
211 372 631 352 2154
196 339 528 380 2078
135 289 409 339 2080
195 334 382 331 2073
118 293 399 311 1758
116 325 343 328 1624
147 311 338 353 1889
154 304 353 518 1988
146 312 289 440 2049
115 283 388 276 1796
161 307 402 207 1720
274 322 151 287 2056
245 335 228 290 1890
201 350 271 355 2187
183 339 440 300 2032
237 327 475 284 1856
175 328 347 337 2068
152 319 449 279 1813
188 325 336 244 1808
188 322 267 253 1834
197 317 235 272 1973
261 315 164 223 1839
232 331 270 272 1935
estimation inference and prediction image 1

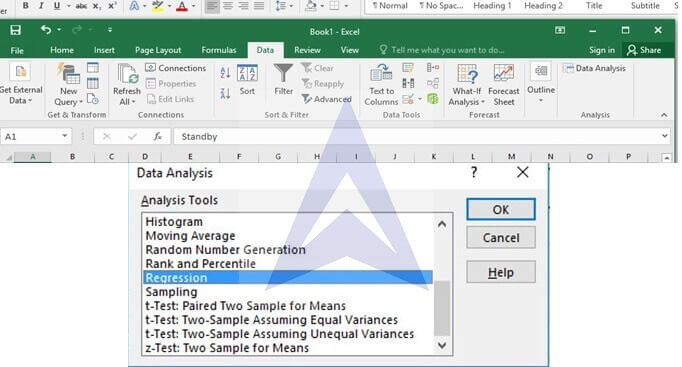
Step 2

Go to data and select the data analysis add in. Click on it and select regression.

estimation inference and prediction image 2

Step 3

  • Select A1 to A27 as y range and B1 to E27 as x range. Click on label so that it can automatically take the first cell of every column as a label and doesn’t produce error results.
  • Click ok to proceed
  • You will find the following table:
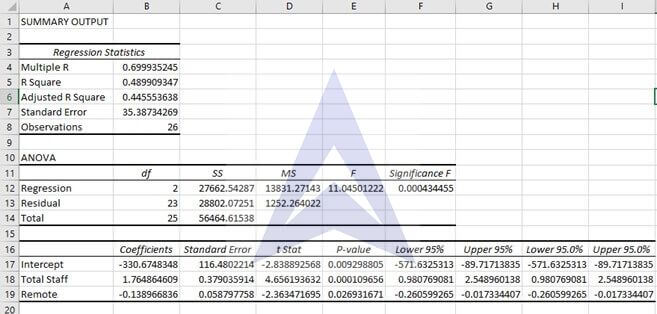
estimation inference and prediction image 3

Now we can answer the question using the table:

A. State the multiple regression equation

From the results obtained we can write the regression equation as follows:

Y = -330.831 + 1.76X1 – 0.13X2
Where, 
Y= standby hours
X1= Total staff present
X2= Remote hours
b0= -330.67
b1= 1.76
b2= -0.13

B. Interpret the meaning of the slopes, b¹ and b², in this problem

The slope b1 means that with a 1 unit increase in total staff present the standby hours increase by 1.76 units.

The slope b2 means that if 1 unit of change is seen in remote hours then the standby hours would decrease by 0.13 units.

Thus we can conclude that standby hours are directly proportional to total staff present while remote hours and standby hours are inversely related.

C. Explain why the regression coefficient, bº, has no practical meaning in the context of this problem

The slope b0 has no practical meaning as time is never negative. And to have an intercept for time is absurd.

D. Predict the standby hours for a week in which the total staff present have 310 people-days and the remote hours are 400

Total staff present = 310
Remote hours = 400
Y=1.76*310 – 0.13*400
= 493.6 hours

E. Construct a 95% confidence interval estimate for the mean standby hours for weeks in which the total staff present have 310 people-days and the remote hours are 400.

Yhat =Y± tn-2,α/2) sY

To calculate t α/2 select the function TINV in excel and put α =0.05 while degree of freedom as 23 (=n-2-1).

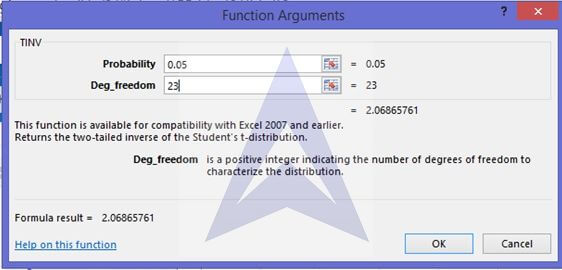
estimation inference and prediction image 4

t23,0.05 = 2.06 
Yhat = 493.6 + (2.06*35.38)
= 566.27
Or Yhat = 493.6 - (2.06*35.38)
= 420.93
Confidence interval = (420.93, 566.27)

Write My Essay Services