Statistics Assignment Help With Properties If Residuals

Property 1:

The sum of the product of any residual of order zero with any other residual of higher order is zero, provided the subscript of the former occurs among the secondary subscripts of the latter.

The normal equations for estimating b’s in trivariate and n-variate distributions as obtained in equations are

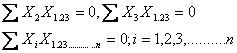
Respectively. Here Xi = (i=1,2,3,……………..,n) can be regard as a residual of order zero. Hence the result.

Property 2:

The sum of the product of any two residuals in which all the secondary subscripts of the first occur among the secondary subscripts of the second is unaltered if we omit any or all of the secondary subscripts of the first. Conversely, the product sum of any residual of order ‘p’ with a residual of order p+q , the ‘p’ subscripts being the same in each case is unaltered by adding to the secondary subscripts of the former any or all the ‘q’ additional subscripts of the latter

Let us consider.

Email Based Homework Help in Properties If Residuals

To submit Properties If Residuals assignment click here.

Following are some of the topics in Correlation and Regression in which we provide help: