Hyperbola Assignment Help

7.7 Hyperbola:

7.7.1 Introduction:In mathematics a hyperbola is a smooth planar curve having two connected components or branches, each being a mirror image of the other and resembling two infinite bows aimed at each other as seen in the figure below. The hyperbola is traditionally described as one of the kinds of conic section or intersection of a plane and a cone, namely when the plane makes a smaller angle with the axis of the cone than does the cone itself , the other kinds being the parabola and the ellipse (including the circle).

A hyperbola is the locus of a point that moves in such a way that the ratio of its distance from a fixed point (known as focus) to its distance from a fixed line(called the directrix) equals a constant e > 1.

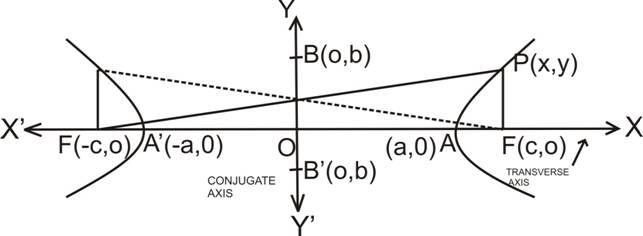
7.7.2 Equation of standard form of Hyperbola: F(c, 0) and F’(c, 0) are the two fixed points, where c > 0. Let P(x, y) be any point on the locus of all points, the difference of whose distances from F and F’ is a positive constant, 2a, where 0 < a < c

|PF – PF’| = 2a

PF – PF’ = ± 2a

√(x – c)² + y² - √(x + c)² + y² = ± 2a

√(x + c)² + y² = √(x – c)² + y² ± 2a

(x + c)² + y² = (x – c)² + y² + 4a² ± 4a √(x – c)² + y²

4cx – 4a² = ± 4a√(x – c)² + y2

(c/a)x – a = ± √(x – c)² + y²

---

Hyperbola Assignment Help By Online Tutoring and Guided Sessions at AssignmentHelp.Net

---

(c²/a²) x² + a² – 2cx = (x – c)² + y²

c² – 1 x² – y² = (c² – a²)

(c² – a²)x² – a²y² = a²(c² – a²)

x²-y² = 1

x² -y² = 1

a² b²

where b² = c² – a²

this is the standard equation of hyperbola.

Length of transverse axis = AA’ = 2a

Length of conjugate axis = 2b

Eccentricity = e = (√a² + b²)/ a

Email Based Assignment Help in Position of A Point With Respect To An Ellipse

To submit Position of A Point With Respect To An Ellipse assignment click here.

Following are some of the topics in Conic Sections-Parabola, Hyperbola And Ellipse in which we provide help: