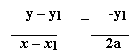Equation Of A Tangent And Normal At A Point

7.5.6 Equation of a tangent and normal at a point

Theorem1 the equation of tangent to the parabola y² = 4ax at the point (x1, y1­) is yy1 = 2a(x + x1) and the equation of normal at this point is 2a(y – y1) + y(x – x1) = 0

Proof: let P(x1, y1) and Q(x2, y2) lie on the parabola y² = 4ax, also we have y1² = 4ax1, y2² = 4ax2

The equation of chord

y – y1 ‗ y2 – y1

x – x1 x2 – x1 …..(i)

Equation Of A Tangent And Normal At A Point Assignment Help By Online Tutoring and Guided Sessions at AssignmentHelp.Net

---

The point P and Q lie on the parabola y2 = 4ax we have y1² = 4ax1 and y2² = 4ax2

y2 – y1 4a

x2 – x1 y1 + y2 ….(ii)

using (i) and (ii) we get the equation of chord PQ as

y – y1 4a

x – x1 y1 + y2

When Q→ P , then x2 → x1 ,y2 → y1 and chord PQ tends to tangent P. hence the equation of tangent at P is given by

y – y1 2a

x – x1 y1

yy1 = 2a(x – x1) + y1² = 2a(x – x1) + 4ax1

yy1 = 2a(x + x1)

this is the required equation of the tangent to the parabola.

The slope of the tangent is given by; 2a

y1

Slope of the normal is given by; -y1

2a

Hence the equation of the normal

Email Based Assignment Help in Equation Of A Tangent And Normal At A Point

To submit Equation Of A Tangent And Normal At A Point assignment click here.

Following are some of the topics in Conic Sections-Parabola, Hyperbola And Ellipse in which we provide help: