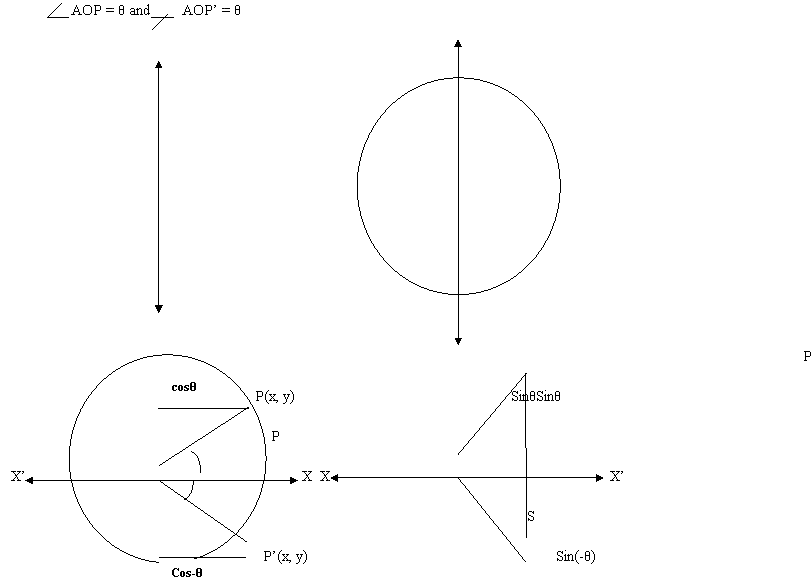Math Assignment Help With Tangent Function

9.7 Tangent function

The figure is a unit circle, with origin O as center cuts the x-axis at A (1, 0) and let a variable point moving on the circumference move through an arc length q. i.e., AP = p (q). The coordinates at the position of p (q) are p(x, y) = (cos q, sin q).

Then the tangent function is defined in the form as

Tanθ = y/x where x ≠ 0

Tanθ = sinθ/ cosθ, where cosθ ≠ 0

X = 0 or cosθ = 0 for θ = (nπ + π/2), where n is an integer. Therefore tanθ is defined for all θ€R except

θ = (nπ + π/2), n€ Z

Therefore, the domain of the tanθ is R’ = R – (nπ+π/2); n€ Z

Theorem1. Sin²θ + Cos²θ = 1

Proof: Let X’OX and Y’OY be the coordinate axes and O being the center. Draw a circle of unit radius cutting OX at A. Let a moving point starts from A, moving along the circumference of the circle. Let its final position be P (x, y), and arc AP=θ.

We know that the equation of the circle is x² + y² = 1

Since the point P (Cosθ, Sinθ) lies on it, therefore

Cos²θ + Sin²θ = 1

Theorem3. Let XOX' and YOY' be the rectangular coordinate axes. Taking O as center and radius = 1, draw a circle to cut x-axis at A and A' and y-axis at B and B'. Let the rotating line start from OA revolving in anticlockwise direction and taking the final position p (x,y) so that arc AP = θ.

On the other hand, if the point starts from A and moves in clockwise direction through arc length AP’ equal arc length AP, then

AP’ = -θ

therefore,

$tangent function$

Join P and P'. Triangles POM and P'OM are congruent.

\ PM = MP'. If PM = y then P'M = -y.

From the DPOM, sin q = y and cos q = x

In D P'OM, sin (-q) = -y and cos (-q) = x

sin(-θ) = -sin θ

cos(-θ) = cos θ

Theorem4. Let x and y be any two real numbers and let P(x)and Q(y) be the corresponding trigonometric points on the unit circle. In the above figures we have taken x and y so that

π/2 < y< x <π

The coordinates of P(x) are (cosx, sin x) and that of Q(y) are (cos y, sin y) by the definitions of cosine and sine functions.

Now choose a point R on the unit circle so that arc AR has a measure of (x-y) units. Then the trigonometric point with respect to (x-y) is R(x-y) and the corresponding coordinates of R are (cos(x-y),sin(x-y)). The arc length of AR is the same as arc PQ and hence the chord lengths of PQ and AR are same.

i) |AR| = distance from R to A.

Using distance formula

[d² = (x1 – x2)² + (y1 – y2)²]

|AR|² = [cos(x – y) – 1]²+ [sin(x – y) – 0]²

= cos²(x – y) – 2 cos(x – y) + 1 + sin² (x – y)

= [cos² (x – y) + sin² (x – y)] – 2 cos(x – y) + 1

= 1 – 2 cos(x – y) +1

= 2 – 2cos(x – y) …..(i)

|PQ|² = (cosx – cosy)² + (sinx – siny)²

= cos²x – 2cosxcosy+cos²y +sin²x +2sinxsiny + sin²y

= (cos²x + sin²x) + (cos²y + sin²y) – 2[cosxcosy + sinxsiny]

= 1 + 1 - 2[cosxcosy + sinxsiny]

= 2 - 2[cosxcosy + sinxsiny] ….(ii)

Since AR = PQ, therefore,

2 – 2cos(x – y) = 2 -2[cosxcosy + sinxsiny]

-2 cos(x – y) = -2[cosxcosy + sinxsiny]

cos(x – y) = cosxcosy +sinxsiny

ii) cos(x+y)

= cos[x – (-y)]

= (cosx) (-y) + (sinx) (-y)

= xcosy + [-sinxsiny] [since cos(-x) = cosx & sin(-y) = -siny]

= cosxcosy - sinxsiny

Theorem5. Proof: i) cos( π/2 – x) = sinx

cos (π/2 – x) = cos (π/2)cosx + sin(π/2)sinx

= 0 +(1) sinx

= sinx

ii) sin(π/2 – x) = cosx

sin(π/2 – x) = cos[π/2 – (π/2 – x)] [since cos(π/2 – θ) = sinθ]

= cosx

iii) cos(π/2 +x) = -sinx

cos(π/2 + x) = cos π/2cosx - sin π/2sinx

= 0 – (1) sinx

= - sinx

iv)sin(π/2 + x) = cosx

sin(π/2 + x) = sin[π/2 – (-x)]

= cos(-x)

= cosx

Theorem 8

For all real values of x.

i) cos(π – x) = -cosx

Proof: cos(π – x) = cosπ cosx + sinπ sinx

= (-1)cosx + 0 sinx

= - cosx

ii) sin(π – x) = sinx

Proof: sin(π – x) = sin[(π/2) + (π/2) – x]

= sin[(π/2) + (π/2 – x)]

= cos(π/2 – x)

= sinx

iii) cos(π+x) = -cosx

Proof: cos(π+x) = cosπcosx – sinπsinx

= (-1)cosx – (0)sinx

= -cosx

iv) sin(π + x) = -sinx

Proof: sin(π + x) = sin [(π/2) + (π/2 + x)]

= cos(π/2 +x)

= - sinx

Theorem 9

For real values of x

i) cos(2π+x) = cosx

Proof: cos(2π+x) = cos2πcosx – sin2πsinx

= (1)cosx – (0)sinx

= cosx

ii)sin(2π+ x) = sinx

Proof : sin(2π+ x) = sin [π + (π + x)]

= - [-sin(π+x)]

= - [-sinx]

= sinx

Theorem 10

i)sin(x+y) =sinxcosy + cosxsiny

Proof: sin( x+y) = cos[π/2 – (x +y)]

= cos[(π/2 – x) – y]

= cos(π/2 – x) cosy + sin(π/2 – x) siny

= sinxcosy + cosxsiny

ii) sin(x – y) = sinxcosy - cosxsiny

Proof: sin(x – y) = sin[x + (-y)]

= sinxcos(-y) + cosxsin(-y)

= sinxcosy – cosxsiny

Theorem 11

i) sin2x = 2sinxcosx

Proof: Consider

sin(x+y) = sinxcosy + cosxsiny

Now put x = y, then

Sin(x + x) = sinxcosx + cosxsinx

Sin2x = 2 sinx cosx

ii) cos2x = cos²x – sin²x = 2cos²x – 1 = 1 – 2sin²x

Proof; take,

cos(x+y) = cosxcosy – sinxsiny

now place x = y,

cos(x+x) = cosxcosx – sinxsinx

= cos²x – sin²x

= cos²x – (1 - cos²x)

= 2cos²x – 1

= 2(1 – sin²x) – 1

= 1 - 2 sin²x

iii) sin3x = 3sinx – 4 sin³x

Proof:we can write,

Sin3x = sin(2x + x)

= sin2xcosx + cos2xsinx

= (2sinxcosx) cosx + (1 – 2sin²x) sinx

= 2sinx cos²x + sinx – 2 sin³x

= 2sinx – 2sin³x + sinx – 2 sin³x

= 3sinx – 4sin³x

iv)cos3x = 4 cos³x – 3cosx

Proof: cos3x = cos(2x + x)

= cos2xcosx – sin2xsinx

= (2cos²x – 1) cosx – 2sinxcosxsinx

= 2 cos³x – cosx – 2cosxsin²x

= 2 cos³x – cosx – 2cosx(1 - cos²x)

= 2cos³x – cosx – 2cosx + 2cos³x

= 4cos³x – 3cosx

Theorem 12

i) 2sinx cosy = sin(x + y) + sin(x – y)
ii) 2cosx siny = sin(x + y) – sin(x – y)
iii) 2cosx cosy = cos(x + y) + cos(x – y)
iv) 2sinx siny = cos(x – y) – cos(x + y)

Proof:

The domain of the tangent function is R’ = R - nπ +π/2 : nϵ Z

Adding (1) and (2)

sin(x+y) + sin(x – y) = 2 sinx cosy ….(i)

Subtracting 2 from 1

sin(x+y) - sin(x – y) = 2 cosx siny ….(ii)

Consider cos(x+y) = cosx cosy – sinx siny …..(3)

And,

cos(x – y) = cosxcosy +sinxsiny ….(4)

Adding (3) & (4)

cos(x + y) + cos(x – y) = 2cosxcosy ….(iii)

Subtracting (4) from (3)

cos(x + y) – cos(x – y) = - 2sinxsiny

cos(x – y) – cos(x + y) = 2sinxsiny …(iv)

Theorem 13

i) 1 – cosx = 2sin²(x/2)

Proof: Consider

cosx = cos(x/2 + x/2) = cos [2(x/2)]

= cos² (x/2) – sin²(x/2)

= 1 – sin²(x/2) – sin²(x/2)

cosx = 1 – 2sin²(x/2)

1 – cosx = 2sin²(x/2)

ii) 1 + cosx = 2cos²(x/2)

Proof: cosx = cos(x/2 + x/2) = 2cos[2(x/2)]

= cos² (x/2) – sin²(x/2)

= cos²(x/2) – [1 – cos²(x/2)]

cosx = 2 cos²(x/2) – 1

1 + cosx = 2 cos²(x/2)

Theorem 14

i) sinx + siny/2 = 2 sin (x + y) cos(x – y)/2

ii) sinx + siny/2 = 2 cos (x + y) sin(x – y)/2

iii) cosx + cosy/2 = 2 cos(x+y)sin(x – y)/2

iv) cosx - cosy/2 = - 2 sin(x+y)sin(x – y)/2

Proof:

Sin(A+B) = sinAcosB +cosAsinB ….(a)

Sin(A – B) = sinAcosB – cosAsinB ….(b)

Adding (a) and(b)

Sin(A+B) +sin(A – B) = 2sinAcosB

Let A+B = x and A – B = y

Then,

A = x + y/2 and B = x – y/2

Therefore,

sinx + siny/2 = 2 sin (x + y) cos(x – y)/2 ….(i)

Subtracting (b) from (a)

sin(A + B) – sin(A – B) = 2cosAsinB

sinx + siny/2 = 2 cos (x + y) sin(x – y)/2 ….(ii)

Now take,

cos(A + B) = cosA cosB – sinA sinB ….(c)

cos(A – B) = cosA cosB + sinA sinB …(d)

adding ( c) and (d)

cos(A + B) + cos(A – B) = 2 cosA cosB

cosx + cosy/2 = 2 cos(x+y)sin(x – y)/2 ….(iii)

Subtracting (d) from ( c)

cos(A + B) – cos(A – B) = -2sinAsinB

cosx - cosy/2= - 2 sin(x+y)sin(x – y)/2 ….(iv)

Theorem 15

i) Sin(x +y) sin(x – y) = sin²x – sin²y

Proof:

sin(x + y)sin(x – y)

= (sinx cosy + siny cosx)(sinx cosy – cosx siny)

= sin²x cos²y – sin²y cos²x

= sin²x (1 – sin²y) – sin²y(1 – sin²x)

= sin²x – sin²x sin²y – sin²y + sin²x sin²y

= sin²x – sin²y

ii) cos(x + y) cos(x – y) = cos²x – cos²y

Proof:

cos(x+y) cos(x – y)

= (cosx cosy – sinx siny) (cosx cosy + sinx siny)

= cos²x cos²y – sin²x sin²y

= cos²x (1 – sin²y) – sin²y(1 – cos²x)

= cos²x – cos²x sin²y – sin²y + sin²y cos²x

= cos²x – cos²y

Email Based Assignment Help in Tangent Function

To submit Tangent Function assignment click here.

Following are some of the topics in Trigonometry in which we provide help:

Not the Exact Question you were looking for? Post your question for assignment help and get instant help on your homework and assignment questions from our experts.