Math Assignment Help With Multiplication Of Vectors

2.7 Multiplication of Vectors

2.7.1 Multiplication by Scalar: Let a be a vector quantity and ά be a scalar quantity. Then,

b = ά a

is a vector quantity having direction parallel to a and its magnitude is given by;

|b| = ά |a|

A unit vector n parallel to a is given by;

--
|a|

2.7.1.1 Product of vector and scalar in Cartesian components:<

a = a_xi + a_yj + a_zk

similarly,

b = b_xi + b_yj + b_zk

and we have,

b = ά a

therefore,

b_xi + b_yj + b_zk = ά (a_xi + a_yj + a_zk) = ά a_xi + ά a_yj + ά a_zk

hence,

b_x = ά a_x b_y = ά a_y ; b_z = ά a_z

2.7.2 Vector products: Two other powerful methods that provide easy working with vectors are the dot (or inner) product and the cross product. The dot product produces a scalar and the cross product operates only on 3−dimensional vectors and produces another vector.

2.7.2.1 Dot Products: The scalar product of two vectors A and B is denoted by

A · B.

The scalar product is also called the dot product.

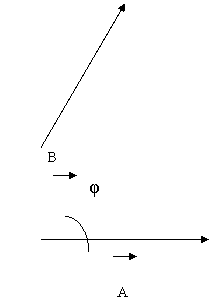
To define the scalar product A · B of two vectors A and B, draw the two vectors with their tails at the same point as shown in the figure below.

The angle between their directions is φ as shown; the angle φ always lies between 0° and 180°. (As usual, we use Greek letters for the angles.) The figure below shows the projection of vector B onto the direction of A;

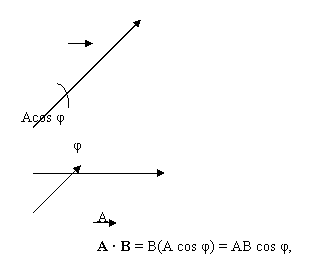
This projection is the component of B parallel to A and is equal to B cos φ.

We define A · B to be the magnitude of A multiplied by the component of B parallel to A

A · B = AB cos φ = |A||B|cos φ

where φ ranges from 0° and 180°.

Alternatively, we can define A · B to be the magnitude of B multiplied by the component of A parallel to B,

which is the same as the previous equation above.

When φ is between 0° and 90°, the scalar product is positive.

When φ is between 90° and 180°, it is negative.

When φ = 90°, A · B = 0. The scalar product of two perpendicular vectors is always zero.

For any two vectors A and B,

AB cos φ = BA cos φ.

This means that

A · B = B · A.

The scalar product follows the commutative law of multiplication; the order of the two vectors does not matter.

The scalar product can also be expressed in terms of components as follows:

A · B = A_xB_x + A_yB_y + A_zB_z

The dot product is distributive:

a.(b + c) = a.b + a.c
and commutative:
a.b = b.a

The angles between i, j, and k vectors is π/2 radians (90 degrees) and cos π /2 = 0, we can derive a handy alternative definition: Let,
u = ai + bj + ck
v = xi + yj + zk
then,
u.v = (ai + bj + ck).( xi + yj + zk)
=>u.v = (ai + bj + ck). xi + (ai + bj + ck).yj + (ai + bj + ck).zk

The angle between any nonzero vector and itself is 0, and cos 0 = 1, so i.i = 1 etc., Hence,

u.v = a x + b y + c z

This means that for any vector, a,
a. a = a²

Email Based Homework Help in Multiplication Of Vectors

To submit Multiplication Of Vectors assignment click here.

Following are some of the topics in Vectors in which we provide help: