Joint Probability Distribution Function Assignment Help

let (X, Y) be a two dimensional random variable then their joint distribution function is denoted by FXY (X,Y) and it represents the probability that simultaneously the observation (X,Y) will have the property (X ≤ x and Y ≤ y) that is

FXY (X,Y) = P( -∞ <X ≤ x, -∞ < Y ≤ y)

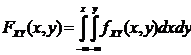
Where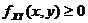

And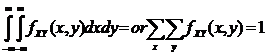

Properties of joint distribution function:

1. 1. for the real numbers a1, b1, a2 and b2

---

Joint Probability Distribution Function Assignment Help By Online Tutoring and Guided Sessions at AssignmentHelp.Net

---

P(a1 < X ≤ b1, a2 < X ≤ b2) = FXY (b1, b2) + FXY (a1, a2) - FXY (a1, b2) - FXY (b1, a2)

1. 2. F (-∞, y) = 0 = F(x, +∞), F(-∞,+∞) =1
2. 3. If the density function 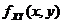is continuous at (x,y) then

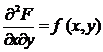
Email Based Homework Help in Joint Probability Distribution Function

To submit Joint Probability Distribution Function assignment click here.

Following are some of the topics in Random Variable And Distribution Function in which we provide help: