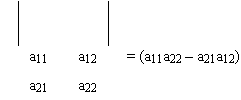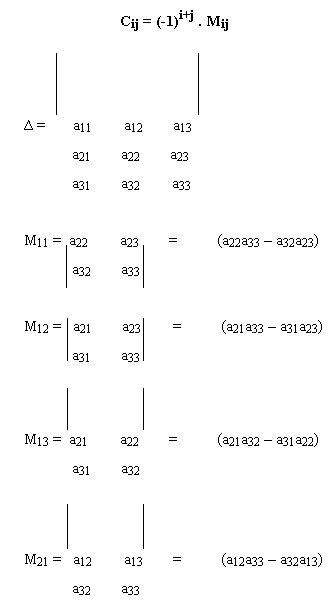Math Assignment Help With Introduction To Determinants

3.6 Introduction to Determinants:

The value of determinant of a(1x1) matrix [a] is defined as |a| = 1

Value of determinant of order 2 is defined as

Value of determinant of order 3 or more is determined by finding minor of aij in |a| and co-factor in aij in |a|.

Minor of aij in |a| is defined as the value of the determinant obtained by deleting the i^th row and j^th column of |A| and is denoted by Mij.

Co-factor of aij in |A| is defined as

Similarly, we can obtain the minor of each one of the remaining elements.

Now if we denote the co-factor of aij by cij, then,

C11 = (-1)¹⁺¹. M11 = (a22a33 – a32a23);

C12 = (-1)¹⁺². M12 = -M12 = (a31a23 – a21a33)

C13 = (-1)¹⁺³. M13 = M13 = (a21a32 – a31a22)

C21 = (-1)²⁺¹. M21 = - M21 = (a32a13 – a12a33)

Similarly, the co-factor of each one of the remaining elements of ∆ can be obtained.

Email Based Homework Help in Introduction To Determinants

To submit Introduction To Determinants assignment click here.

Following are some of the topics in Matrices And Determinants in which we provide help: