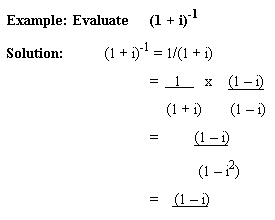Math Assignment Help With Division Properties

1.6.3 Division properties:

While dividing two complex numbers,

write the problem in fractional form,

Rationalize the denominator by multiplying the numerator and the denominator by the conjugate of the denominator

Division properties are fundamental mathematical concepts that describe the rules and relationships associated with division, one of the four basic arithmetic operations. Division allows us to distribute or partition a quantity into equal parts or groups. Understanding division properties is crucial in various mathematical applications, including solving equations, working with fractions, and simplifying expressions.

Here are some essential division properties and an introduction to each:

1. Division as the Inverse of Multiplication: Division is the inverse operation of multiplication. This means that if you have a multiplication problem like 3 x 4 = 12, you can use division to undo it: 12 ÷ 3 = 4 or 12 ÷ 4 = 3. This property forms the basis for solving equations and understanding the relationship between multiplication and division.

2. Division by Zero: Division by zero is undefined in mathematics. You cannot divide any number by zero, as it does not result in a meaningful or well-defined value. For example, 5 ÷ 0 is undefined.

3. Quotient: The result of a division operation is called the quotient. In the division expression a ÷ b = c, 'a' is the dividend, 'b' is the divisor, and 'c' is the quotient.

4. Remainder: In some division operations, there may be a remainder. For example, when dividing 10 by 3, you get a quotient of 3 and a remainder of 1. This concept is often used in modular arithmetic and can be represented using the modulo operator (%).

5. Division of Fractions: Division of fractions involves multiplying the first fraction by the reciprocal (flipped version) of the second fraction. For example, (1/2) ÷ (1/4) is equivalent to (1/2) * (4/1) = 2.

6. Associative Property: Division is not associative, which means that the grouping of numbers in a division expression affects the result. For example, (10 ÷ 2) ÷ 5 is not the same as 10 ÷ (2 ÷ 5). The former equals 5, while the latter equals 25.

7. Commutative Property: Division is not commutative, meaning that the order of the numbers matters. In general, a ÷ b is not the same as b ÷ a. For example, 10 ÷ 2 is not the same as 2 ÷ 10. The former equals 5, while the latter equals 1/5.

8. Identity Property: Just like multiplication has an identity element (1), division has its identity element (dividing by 1). Any number divided by 1 remains unchanged. For example, a ÷ 1 = a for any real number 'a.'

Understanding these division properties is essential for performing accurate calculations and solving various mathematical problems involving division. These properties provide a foundation for more advanced mathematical concepts and applications in algebra, calculus, and beyond.

Email Based Homework Help in Division Properties

To submit Division Properties assignment click here.

Following are some of the topics in Complex Number in which we provide help: