Sampling Theory
Given a normally distributed population, a sampling distribution is summarized by μX = 300 and σX = 28. What is the probability that a simple random sample will reveal a sample mean a. below 200? b. between 200 and 265? c. above 346?
Given –
Sample mean = 300
Standard error = 28
a) P(X̅<200)
= P(X̅-300/28 < 200-300/28)
= P(z ≤ -3.57)
= 0.000178
b) P (200<X̅<265)
= P ( X̅ < 265 ) – P( X̅ < 200 )
= P ( X̅-300/28 < 265-300 /28) – P( X̅ - 300 /28 > 200 -300/28)
= P (z<-1.25) – P(z< -3.57)
= P(z>1.25) – P(z> 3.57)
= [1 – P(z<1.25)] – [( 1 – P(z<3.57) )]
= (1 - .8944) – (1 -0.9998)
= 0. 1054
C) P(X̅ > 346)
= 1- P(X̅ ≤ 346)
= 1- P( (346 – 300)/28)
= 1- P (1.643)
= 0.050191
A normally distributed population of 12 oz. beer cans has a mean of 105 calories and a standard deviation of 3 calories. Compute the mean of a sampling distribution for a simple random sample of 30 as well as the associated standard error.
Population mean = 105 oz
Population standard deviation = 3 oz
n = 30 oz
Mean of sampling distribution = E(X̅ ) = µ = 105 oz
Standard error = Standard deviation / √n
= 3/√30
= 0.5477
The daily lunch expense of corporate executives is a normally distributed random variable with a mean of £9.9 and a standard deviation of £1. Describe the sampling distribution of the mean for a simple random sample of n = 36. What is the probability of encountering a sample mean between £10 and £11?
Probability of encountering a sample mean between £10 and £11 = P(10≤x̅≤11)
= P(10 – E(X̅)/Standard error ≤ x̅ - E(X̅)/Standard error ≤ 11 - E(X̅)/Standard error )
= Standard error = Standard deviation / √n
= 1/√36
= 1/6
= 0.16667
P (10 – 9.9/ 0.16667 ≤ x̅ - 9.9/ 0.16667 ≤ 11- 9.9/ 0.16667)
= P (0.599 ≤ z ≤ 6.59)
= P (z≤6.59) – P (z≤0.599)
= 1- 0.274586 (since for any Z greater than 4 we assume Probability to be equal to 1)
= 0.725414 or 72.54%
An investigator knows that the population of light bulb lifetimes is normally distributed and that the standard deviation is 36 hours. A simple random sample of 49 bulbs discloses a sample mean lifetime of 510 hours. Determine a 95% confidence interval for the mean lifetime of all such bulbs.
Population standard deviation = 36
n = 49
X̅ = 510
Confidence level = 95% = 1 - α
We know
µ = X̅ ± Zα/2 * Standard Error of X̅
Z_(α/2)=1.96 (from normal distribution table)
Standard Errors of X̅ = Population standard deviation/√n
= 36/√49
= 5.1428
It implies µ = 510 ± 1.96 (5.1428)
= 499.92 ≤ µ ≤ 520.08
A banker who believes the relevant statistical population to be normally distributed wants to estimate the average monthly mortgage payment in a city. A simple random sample of 28 homeowners produces a mean of £426.73 with a standard deviation of £29.75. Determine a 99.8% confidence interval for the citywide average monthly payment.
Sample standard deviation = S = 29.75
n = 28
X̅ = 426.75
Confidence level = 99.8% = 1 – α
We know
µ = X̅ ± Zα/2 * Standard Error of X̅
Zα/2=0.5839(from normal distribution table )
Standard Error of X̅ = Sample standard deviation/√n
= 29.75/√28
= 5.6627
It implies µ = 426.73 ± 0.5839(5.6627)
= 410.25 ≤ µ ≤ 444.10
Passengers abandoning a sinking liner have a mean weight of 77kg, with a standard variation of 8kg. 40 passengers clamber onto a lifeboat, which will capsize if the total weight of the passengers exceeds 3,200kg. What is the probability that the lifeboat will capsize?
Population mean = µ = 77 kg = E(x̅)
Population Standard deviation = 8 kg
Standard error = Population Standard deviation/ √n
Total passengers = 40
Average weight of 1 passenger for lifeboat to capsize with 40 persons = 3200/40 = 80
Standard Error of weights of Passenger
= 8/√40
= 1.265
n = 40
Probability of boat capsizing = P (X̅ ≥ 3200)
= P (X̅ - µ /Standard error of X̅ ≥ 3200 - µ/Standard error of X̅)
= P (Z ≥ 80 – 77/1.265)
= P(z ≥ 2.37)
= 1-P( z ≤2.37)
= 1 - .99111
= 0.00889
A random sample of 65 weekly rents for one-person flats provides the following information: sample mean X = £345, sample deviation s = £32. Find a 98% confidence interval for the true population mean rent. Interpret your result carefully
Sample standard deviation = s = 32
n = 65
X̅ = 345
Confidence level = 98% = 1 - α
We know
µ = X̅ ± Z_(α/2) * Standard Error of X̅
Zα/2=0.2885( from normal distribution table )
Standard Error of X̅ = Sample standard deviation/√n
=32 /√65
= 3.96
It implies µ = 345 ± 0.885 ( 3.96 )
= 335.766 ≤ µ ≤ 354.3323
Interpretation: This means that in 98 out of 100 one-person flats sampled, the mean weekly rent will lie in between £336 and £355
A sample of 100 supermarket shoppers spend on average £56 with a standard deviation of s = £10. Find a 95% confidence interval for the true mean of shoppers’ spending.
Sample standard deviation = S = 10
n = 100
X̅ = 56
Confidence level = 95% = 1 - α
We know
µ = X̅ ± Zα/2 * Standard Error of X̅
Zα/2 = 1.96( from normal distribution table )
Standard Error of X̅ = Sample standard deviation/√n
=10 /√100
= 1
It implies µ = 56± 1.96 (1)
= 54.04 ≤ µ ≤ 57.96
Suppose two economists estimate μ (the average expenditure of British families on food) with two unbiased (and statistically independent) estimates U and V. The second economist is less careful than the first: the standard deviation of V is 3 times as large as the standard deviation of U. When asked how to combine U and V to get a publishable overall estimate, three proposals are made: • W1 = ½ U + ½ V (simple average) • W2 = ¾ U + ¼ V (weighted average) • W3 = 1 U + 0 V (drop the less accurate estimate) (a) Which are unbiased? (b) Which is the best estimator? The worst? (c) Is it possible to find an even better estimator?
W1 = ½ U + ½ V (simple average)
Taking expectation both sides
It implies, E(W1) = ½ E(U) + ½ E(V)
= ½ µ + ½ µ = µ
And E(W1) also equals µ
LHS = RHS
Therefore W1 is unbiased
W2 = ¾ U + ¼ V (weighted average)
Taking Expectation both sides
RHS
E(3/4U+1/4V)
=3/4*E(U)+1/4*E(V)
=3/4µ+1/4*µ
=µ
LHS
E(W2) =µ
HENCE LHS = RHS
SO W2 IS UNBIASED
W3 = 1 U + 0 V (drop the less accurate estimate)
Taking Expectation both sides
RHS
E(1U+0V)
=1*E(U)+0*E(V)
=µ
LHS
E(W3)
=µ
LHS=RHS
HENCE W3 IS UNBIASED
B) W1 = ½ U + ½ V (simple average)
TAKING VARIANCE BOTH SIDES
RHS
V(1/2U+1/2V)
=1/2*1/2V(U)+1/2*1/2V(V)
=1/4V(U)+1/4(9V(U))
=5/2V(U)
W2 = ¾ U + ¼ V (weighted average)
TAKING VARIANCE BOTH SIDES
RHS
V( ¾ U + ¼ V)
=3/42V(U)+1/42V(V)
=9/16V(U)+1/16(9V(U))
=9/8V(U)
W3 = 1 U + 0 V (drop the less accurate estimate
RHS
V(1U+0V)
=1V(U)
It implies W3 is best estimator as it has less variance Also W1 is worst estimator as it has most variance (By Minimum Variance Unbiased Estimator)
(Estimating a population proportion) A random sample of 100 workers in an economy reveals that 20% are unemployed. Obtain an unbiased point estimate of the true population unemployment level. Hence obtain a 99% confidence interval for the true population unemployment level.
n = 100
pˆ = 20% = 0.2
1-α = 99%
We know
P = pˆ ± Zα/2 SD (pˆ)
Where SD (pˆ) is 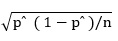
By putting the values it implies
SD (pˆ) = 0.04
Zα/2 = 2.575
Putting the value in formula 1 we get
P = 0.2 ± 2.575(0.04)
0.097 ≤ P ≤ 0.303


