MGMT 472 final exam study questions

Which of the following is not one of the important distinctions of probability distributions?
1. Discrete versus continuous
  1. Symmetric versus skewed
  2. Bounded versus unbounded
  3. Positive versus negative
2. Discrete distributions are sometimes used in place of continuous distributions:
  1. because they are more accurate
  2. because they are simpler
  3. when we don't know the mean and variance of the distribution
  4. when we need to generate a histogram
3. Which of the following statements is true regarding the Triangular distribution?
  1. It is a discrete distribution with a minimum, maximum and most likely value
  2. It is more flexible and intuitive than the normal distribution
  3. It is a symmetric distribution
  4. All of these options
4. The RAND() function in excel models which of the following probability distributions?
  1. Normal distribution with mean 0 and standard deviation 1
  2. Uniform distribution with lower limit 0 and upper limit 1
  3. Normal distribution with mean -1 and standard deviation 1
  4. Uniform distribution with lower limit -1 and upper limit 1
5. A distribution for modeling the time it takes to serve a customer at a bank is probably:
  1. symmetric
  2. left skewed
  3. right skewed
  4. uniform
6. If a model contains uncertain outputs, it can be very misleading to build a deterministic model by using the means of the inputs to predict an output. This is called the:
  1. Law of Large Numbers.
  2. Flaw of Averages
  3. Law of Inevitable Disappointment
  4. Central Limit Theorem
7. One of the primary advantages of simulation models that they enable managers to answer what-if questions about changes in systems without actually changing the systems themselves.
  1. True
  2. False
8. Excel's standard functions, along with the RAND function, can be used to generate random numbers from many different types of probability distributions.
  1. True
  2. False
9. When the value of a decision variable has been optimized by running several simulations, attitude toward risk should no longer be relevant.
  1. True
  2. False
10. It is usually fairly straightforward to predict the shape of the output distribution from the shape(s) of the input distribution(s).
  1. True
  2. False
11. Correlation between two random input variables may change the mean of an output, but it will not affect the variability and shape of an output distribution.
  1. True
  2. False
12. Which of the following functions is not an @RISK statistical function?
  1. RISKMIN
  2. RISKMAX
  3. RISKPERCENTILE
  4. RISKSIMTABLE
13. The RISKSIMTABLE function is used to summarize the results of a single simulation of product lifetime.
  1. True
  2. False
14. A company is considering investing $1.2M in a facility to manufacture a new product. The product will have a five year life, after which the facility will be shut down. A pro forma cash flow sheet for this project, with forecasted production levels, unit prices, and production costs, is shown below:
  
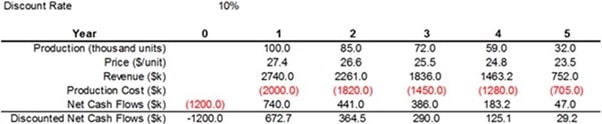
  What is the deterministic next present value (NPV) of the project, including the required investment, assuming a 10% discount rate?
  1. $281,500
  2. $290,000
  3. $311,000
  4. $275,000
15. Refer to the model given in Question 14, assume that the forecasted price levels shown in the pro forma cash flow sheet are not deterministic, but rather are expected to fluctuate due to market forces. The prices are expected to be normally distributed in each year, with the following means and standard deviations:
  Using the appropriate @RISK functions in the pro forma, what is the expected NPV?
  1. $290,000
  2. $270,000
  3. $282,000
  4. $305,000
16. In the model above, what is the standard deviation of the NPV?
  1. $500,000
  2. $650,000
  3. $707,000
  4. $70,000
17. Given your answers in 15-16, would you invest in this project if your risk appetite is low, that is you are essentially risk averse?
  1. Yes I would.
  2. No I would not.
18. We want to choose capacity for a plant that will produce a new drug. In particular, we want to choose the capacity that maximizes discounted expected profit over the next 10 years. Assume all cash flows occur at the end of the year. We have the following information:
  - Demand for the drug is expected to be normally distributed ˜ Normal (50,000, 12,000).
  - Demand each year is an independent event.
  - A unit of capacity costs $16 to build in year 1.
  - The number of units produced will equal the demand, up to capacity limits.
  - The revenue per unit is $3.70 and the cost per unit is $0.20 (variable cost).
  - The maintenance cost per unit of capacity is $0.40 (fixed cost).
  - The discount rate is 10%.
  Perform a simulation assuming the plant will be designed to meet the expected demand. What is the expected net present value (NPV) in this case?
  1. $39,374
  2. $45,474
  3. $49,474
  4. $51,000
19. Using the case in Question 18, make use of RISKSIMTABLE to with the following values for capacity: 20,000, 25,000, 30,000, 35,000, 40,000. Which of these capacities produces the largest expected NPV?
  1. Q=30,000
  2. Q=35,000
  3. Q=25,000
  4. None of them
20. In the simulation model run in Question 19, are there any simulations which indicated there was a chance of getting negative NPV? If yes, at which capacity level do you obtain it?
  1. Q=35,000
  2. Q=20,000
  3. Q=25,000
  4. Q=30,000