Interpret and apply the statistical techniques

Assessment criteria

• This assignment must be typed, word-processed or clearly hand-written (but plots and graphs must be done using EXCEL or equivalent software), and submitted online as a single file through Moodle. Important note: The file size must not be over 50MB.
• Microsoft Excel allows students to cut and paste information easily into Microsoft Word documents. Word also allows the use of Microsoft Equation Editor to produce all necessary formulae (use of these are recommended).
• It is expected that Excel would be used to assist in statistical calculations for questions in this assignment. Where Excel is used, use copy function, “Snipping tool” or similar to cut and paste relevant parts of the spreadsheet to verify that you have done the work.
• For those questions where Excel is not used to do the computations, all formulae and working must be included to obtain full marks.
• Only one file will be accepted in any of the formats mentioned above. No zipped file or any other file extension will be accepted.
• There will be late submission penalty for submissions beyond the deadline unless prior approval is obtained from the Unit Coordinator through the extension system in Moodle. Under no circumstances any submission that is late beyond 14 days from the deadline of Friday of Week 10 will be marked, or get any score other than zero.

Assignment markers will be looking for answers which

• demonstrate the student’s ability to interpret and apply the statistical techniques in the scenarios and
• use statistical techniques as decision making tools in the business environment.

Full marks will not be awarded to answers which simply demonstrate statistical procedures without comment, interpretation or discussion (as directed in the questions).

Plagiarism

CQU values academic honesty. Consequently, plagiarism will not be tolerated in assessment items. This assignment must be completed by each student individually.

Question 1

Visit the Australian Stock Exchange website, asx.com.au and from “Prices and research” drop-down menu, select “Company information”. Type in the ASX code “MQG” (Macquarie Group Limited), and find out details about the company. Also, type in the ASX code “PPT” (Perpetual Limited), and find out the details about that company. Both these companies belong to financial sector. Information available in the ASX website will be inadequate for your purpose, you will need to search the internet for more information. Your task will be to get the opening prices of MQG and PPT shares for every quarter from January 2008 to December 2017 (unadjusted prices). If you are retrieving the monthly prices, read the values in the beginning of every Quarter (January, April, July, October) for every year from 2008 to 2017 (Total 40 observations). To provide you with some guidance as to what the unadjusted prices look like, two charts accompany this question obtained from ANZ Share Investing, Australia. After you have researched share prices and financial sector, answer the following questions:

• List all the quarterly opening price values in two tables, one for MQG and the other for PPT. Then construct a stem-and-leaf display with one stem value in the middle, and MQG leaves on the right side and PPT leaves on the left side. (Must use EXCEL or similar for the plot.) 1 mark
• Construct a relative frequency histogram for MQG and a frequency polygon for PPT on the same graph with equal class widths, the first class being “$0 to less than $10”. Use two different colours for MQG and PPT. Graph must be done in EXCEL or similar software. 1 mark
• Draw a bar chart of market capitals (or total assets) in 2017 (in million Australian dollars) of 6 companies listed in ASX that trade in financials with over AUD500 million in market capital. Graphing must be done in EXCEL or with similar software. 1 mark
• If one wishes to invest in MQG or PPT, what is the market recommendation (for example, from Morningstar, Fatprophets, InvestSmart, etc.)? If you cannot find the information, what would be your recommendation based on your research of these two companies (trend, P/E ratio, dividend yield and Beta)? 1 mark

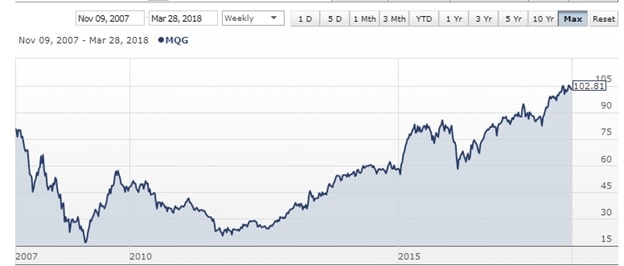
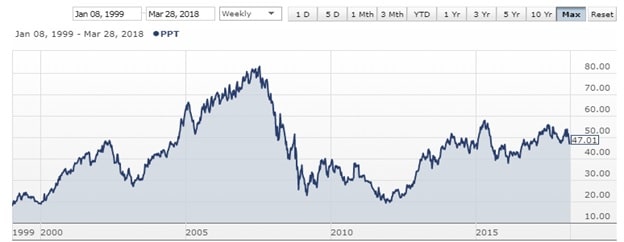
Question 2

Top five telecommunication companies listed in the Australian Stock Exchange in terms of market capital are Telstra Corporation Limited (TLS), Spark New Zealand Limited (SPK), TPG Telecom Limited (TPM), Chorus Limited (CNU) and Vocus Group Limited (VOC). The accompanying table provides the average price-earnings ratio (P/E) for these companies for different years. From the data answer the questions below for these companies. (Work only with the data provided. Missing values indicate data not available for those companies during those years.)

• Compute the mean, median, first quartile, and third quartile of average price-earnings ratio for each company using the exact position, (n+1)f, where n is the number of observations and f the relevant fraction for the quartile. 1 mark
• Compute the standard deviation, mean absolute deviation and range for each company. 1 mark

(Question 2 continued next page)

(Question 2 continued)

• Draw a box and whisker plot for the average price-earnings ratio of each company and put them side by side on one graph with the same scale so that the P/Es can be compared. (This graph must be done in EXCEL or similar software and cannot be hand-drawn.) 1 mark
• Write a paragraph on price-earnings ratio values related to it being indicative of a share being a good investment or a poor investment. 1 mark

Question 3

The Table below is taken from the Australian Bureau of Statistics (ABS) website http://www.abs.gov.au/AUSSTATS/abs@.nsf/DetailsPage/3303.02013?OpenDocument. It provides data on underlying causes of death of Australian population.

Table: Number and causes of deaths in Australia in 2013 (published in 2015).

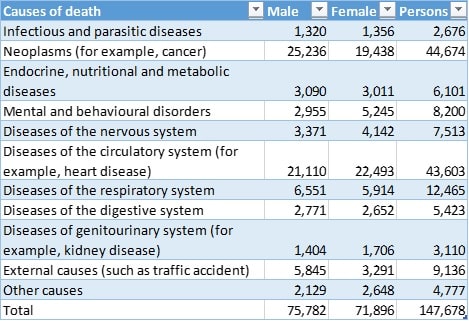
• Based on the table above, what is the probability that an Australian selected at random will die from neoplasms?
• Based on the table above, what is the probability that an Australian selected at random will die from a disease of the circulatory system and is a female?
• Based on the table, which disease has the highest proportion of male deaths compared to female deaths, and also, which disease has the highest proportion of female deaths compared to male deaths?
• Visit the ABS website (Data Cube 1) and determine the probability of an Australian selected at random of dying from diabetes mellitus.

Question 4

• The following data collected from the Australian Bureau of Meteorology Website (http://www.bom.gov.au/climate/data/?ref=ftr) gives the daily rainfall data (includes all forms of precipitation such as rain, drizzle, hail and snow) for the year 2017 in Melbourne, Victoria. The zero values indicate no rainfall and the left-most column gives the date. Assuming that the weekly rainfall event (number of days in a week with rainfall) follows a Poisson distribution (There are 52 weeks in a year and a week is assumed to start from Monday. The first week starts from 2 January 2017 – you are expected to visit the website and get the daily values which are not given in the table below. Part of the 52^nd week may run into 2018.):

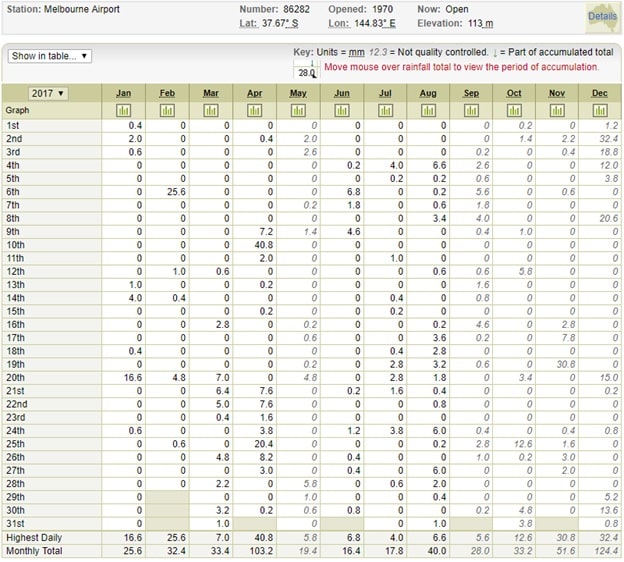
1. What is the probability that on any given week in a year there would be no rainfall?
2. What is the probability that there will be 2 or more days of rainfall in a week?

(b) Assuming that the weekly total amount of rainfall (in mm) from the data provided in part (a) has a normal distribution, compute the mean and standard deviation of weekly totals.

1. What is the probability that in a given week there will be between 5mm and 15mm of rainfall?
2. What is the amount of rainfall if only 10% of the weeks have that amount of rainfall or higher?

Question 5

Download glass data from the UCI machine learning data repository (https://archive.ics.uci.edu/ml/machine-learning-databases/glass/). The dataset is about glass identification based on its properties. The column headings in sequence from first to last are observation number, refractive index, sodium (content in weight percent), magnesium, aluminium, silicon, potassium, calcium, barium, iron and type of glass (last column). From the data provided, answer the questions below.

(a) Test for normality of all the variables separately using normal probability plot, except the first and last column variables.

(b) Construct a 90% confidence interval for each of the variables in part (a) which can be considered as normally distributed separating the data between float glass and non-float glass. In the last column, the numbers 1 and 3 represent float glass, all other numbers indicate non-float glass. In other words, there will be two confidence interval constructions for each normally distributed variable – one for the float glass observations and the other for the non-float glass observations. After all the confidence intervals have been constructed, identify the variable(s) which are significantly different in composition between float and non-float type of glasses (i.e., identify the variables where the confidence intervals do not overlap).