CS 230 Computer Architecture and Assembly Language Assignment 3

Programming environment

For this assignment you must ensure your work executes correctly on the MIPS Assembler and Runtime Simulator (MARS) as was installed during Assignment #0. Assignment submissions prepared with the use of other MIPS assemblers or simulators will not be accepted. Solutions which prompt the user for input will not be accepted.

Objectives of this assignment

• Implement operations for 16x16 byte arrays (i.e., two dimensions, or 2D) using row-major
• Implement a specific operation on such a 2D byte
• Convert an array bitmap patterns (as explored in Lab 9 of this course) into a 2D array of bytes (where “bit set” corresponds to a 1 stored in a specific array location, and “bit unset” corresponds to a 0 stored in a specific array location).
• Render the contents of a 2D byte array (as described above) as on-off pixels on the Bitmap Display
• Write a procedure that will implement the “Game of Life” by using work fulfilling the previous objectives for this
• Produce an “Instruction Statistics” report for code written in this final

Provided with this assignment on conneX is an HTML file containing a link to video demonstrating the behavior of all some (but not all!) parts of this assignment.

This assignment is designed in such a way that each part builds on those completed earlier. Please read all of the assignment before starting work. You do not necessarily need to understand all of the description before starting work. In fact, some of the later parts will make more sense to you as you complete earlier parts.

In order to ensure that your work on later parts does not break successful work on earlier parts, each of the parts for this assignment is submitted in a separate .asm file.

Part 1: 2D byte arrays (16x16)

set_16x16

parameters:

$a0 holds the address of first byte in the array

$a1 holds the row index

$a2 holds the column index

$a3 holds a word whose right-most byte is to be stored in the array at the row index, column index

return value: none

comment: If the provided row index or column index (or both) are out of range, there is no effect on the computer’s memory.

get_16x16

parameters:

$a0 holds the address of first byte in the array

$a1 holds the row index

$a2 holds the column index

return value: $v0 holds the value of the byte currently stored in the array at the row and column

comment: If the provided row index or column index (or both) are out of range, a value of 0 is returned in $v0.

copy_16x16

parameters:

$a0 holds the address of first byte in the destination array $a1 holds the address of first byte in the source array return value: none

File that must be used: a4-part-1.asm

Two-dimensional arrays are an abstraction provided to programmers. In reality all memory is one-dimensional – that is, a 32-bit computer’s memory consists of an array of bytes starting from index/address 0x00000000 and going up to index/address 0xffffffff. However, many kinds of problems are much easier to solve as a computer program if we can not only think in terms of two-dimensional (2D) arrays, but also express our solution in a way that directly uses the row and column indexes of a 2D array.

For example, below is a representation of a 16-byte one-dimensional array:

The element with value 53 is indexed at 6; the element with value 84 is indexed at 12. Notice also that we use 0 to index the first element in this array.

However, we could also represent the given data as a four-by-four 2D array:

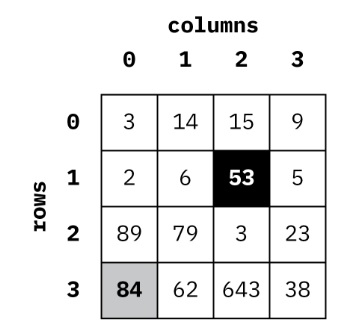
Notice now the element with value 53 is indexed as row 1, column 2; the element with value 84 is indexed as row 3, column 0.

The curious thing is that both figures represent exactly the same memory!

2D arrays are often implemented in what is known as row-major order. That is, the contents of each row are laid down, one after the other, in a 1D array. Calculating the location of a 2D element in a 1D array where row-major order is used is therefore straightforward.

Assume rowlength is 4:

• Element with value 53: row 1, column 2: 1 * rowlength + 2 = 6
• Element with value 84: row 3, column 0: 3 * rowlength + 0 = 12

You are to complete the three procedures for this Part 1 such that row and columns can be used to read (i.e., get_16x16) and write (i.e., set_16x16) values in a 16x16 2D array of bytes (i.e., where rowlength is 16 bytes). For completeness you will also write a procedure copy_16x16 to make a copy of an 2D byte array (of size 16x16) in a different area in memory.

Part 2: A typical operation using 2D array

sum_neighbours

parameters:

$a0 holds the address of first byte in a 16x16 array of bytes

$a1 holds the row index

$a2 holds the column index

return value: $v0 holds the sum of array elements directly neighbouring given row & column element.

File that must be used: a4-part-2.asm

In part 1, a motivation for 2D array operations was suggested. That is, sometimes it is easier to think in terms of 2D arrays and to write solutions using 2D operations.

Below is a representation of some possible 16x16 byte array. (The data was randomly generated, so there is significance to the values.)

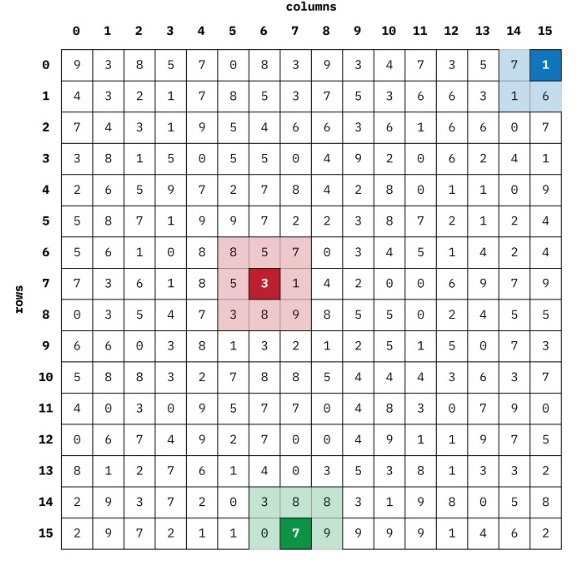
Consider the element at row 7, column 6. This element has eight neighbours with values (starting at 12 o’clock and going clockwise) of 5, 7, 1, 9, 8, 3, 5, and 8, which all sum to 46.

Now consider the element at row 15, column 7. This element is at one “edge” of the array (so to speak), such that it has fewer neighbours. However, if we were to treat the “missing neighbours” as having values of 0, then (starting at 12 o’clock and going clockwise) we would have the values 8, 8, 9, 0, 0, 0, 0, and 3, which all sum to 28.

Finally consider the element at row 0, column 15. This element is at a “corner” of the array (so to speak). If we were again to treat the “missing neighbours” as having values of 0, then (starting at 12 o’clock and going clockwise) we would have the values 0, 0, 0, 0, 6, 1, 7, and 0, which all sum to 14.

You are to complete the single procedure sum_neighbours for this Part 2 such the values of the neighbours around a given element in some 16x16 byte array are added together and this value returned. The element’s location is given by its row and column. You are permitted to copy-and-paste work from your complete Part 1 as part of your solution to Part 2.

Part 3: Bitmaps, 2D byte arrays, and the Bitmap Display tool

bitmap_to_16x16

parameters:

$a0 holds the address of first byte in the array

$a1 holds the address of the first word holding a row’s bitmap pattern return value: none

draw_16x16

parameters:

$a0 holds the address of first byte in the array return value: none

File that must be used: a4-part-3.asm

In one of the later labs this semester, you learned how the individual bits in a 32-bit word can be used to represent whether or not a pixel is on or off in the Bitmap Display tool. (More precisely, the right-most 16 bits of a word is used to represent the pattern of on-off pixels for one row in the 16x16 bitmap display.) Consider the following diagram:

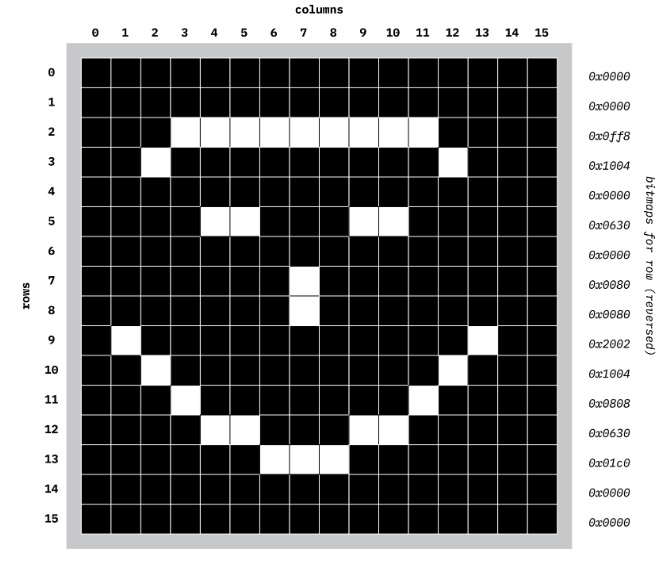
Each element in a row is dark if the pixel is unset, and is light if the pixel is set. We may represent this figure by a 16x16 byte array. For example, the byte at row 5, column 10, will have the value 1; the next element to the right at row 5, column 11 will have the value 0.

Your task is in this part is twofold. You are to write bitmap_to_16x16 which will take 16 row-bitmap patterns (i.e., stored in 16 consecutive 32-bit words) and convert these into values of 0 and 1 for some given 2D 16x16 byte array. You will also write draw_16x16 which will take a given 2D 16x16 byte array, and where an element (row, column) in the array has the value of 1, the corresponding pixel in the Bitmap Vector (at that row, column) will be set to white; if the value in the array is 0, the corresponding pixel will be set to black. You are permitted to copy-and-paste work from previous completed parts of this assignment iton your solution to Part 3.

Part 4: The “Game of Life”

life_next_generation parameters: nonereturn value: none

File that must be used: a4-part-4.asm

The mathematician John Conway became famous in 1970 when his “Game of Life” was published in an issue of the Scientific American. Your task in this part is to combine your work for the previous parts of this assignment into an implementation of this game. (Sadly, Dr. Conway died in April 2020 from complications of COVID-19.)

Strictly speaking this is not a game where the user interacts with the computer. Rather, some starting value of on-off values in a 2D array (such as would result from calling bitmap_to_16x16) is used to compute the “next generation” of 16x16 values. Each successive generation is displayed. An element is “alive” if the value of the element is 1; the element is “dead” if the value of the element is 0.

In order to compute the next generation from the current generation, there are three rules:

1. If an element is alive in the current generation, and if the element has exactly two or three neighbours who are alive, then in the element is alive in the next generation (i.e., it goes from “alive” to “alive”).

2. If an element is alive in the current generation, and if the element exactly one neighbour, or has four or more neighbours, then that element is dead in the next generation (i.e., it goes from “alive” to “dead”).

3. If an element is dead in the current generation, and if the element has exactly three neighbours who are alive, then in the next generation that element is alive (i.e., it goes from “dead” to “alive”). Otherwise the element remains dead (i.e., it goes from “dead” to “dead”).

If you are curious for more information about Conway’s game, then have a look at the Wikipedia article (which is very complete) at: https://bit.ly/2ODGlpi

In code provided for you in this part, the main code performs the following steps:

• The 16x16 byte array GEN_A is initialized to values of 0 or 1 based on an existing bitmap pattern (e.g., PATTERN_GLIDER).
• The GEN_A byte array is drawn on the Bitmap Display
• The procedure life_next_generation is called, and it is assumed that when the procedure returns, the value of the next generation of 0 or 1 values is stored into GEN_A.
• The GEN_A byte array is draw on the Bitmap Display Then the code loops back to the previous step (i.e., infinite loop, moving from generation to generation).

You are to complete the code for life_next_generation. It is very important that this procedure does not itself call the set_pixel procedure. That is, the architecture of this solution depends upon separating the computation of the next generation from its rendering on the Bitmap Display tool. You are permitted to copy-and-paste work from previous completed parts of the assignment in your solution to Part 4.

(Thanks to David Clark for creating a “proof-of-concept” for this assignment idea.)

Part 5: Some instruction statistics and rudimentary analysis

Towards the end of the course we have been looking at ways in which computer system architects improve the performance of the systems. In order to determine whether or not improvement is possible, measurement is needed of either some simulated design or of an actual system.

MARS provides an Instruction Statistics tool. You are to use this to find and record statistics for the kinds of instructions used by actually-running procedures from parts 1, 2 and 3 from this assignment. (Because the tool slows down MARS, it isn’t entirely practical to get statistics for part 4, although you are welcome to experiment here).

For each of the procedures, you are to:

• Indicate the tests that was used for that procedure
• Record the instruction statistics from the test runs (both individual and in the aggregate)

It will, of course, be the case that procedures written earlier in the assignment will be used by procedures used later in the assignment. So you are also to:

• Write a paragraph analyzing the relationship of instruction-count statistics (e.g., how do the statistics for a run of sum_neighbours relate to the statistics for a run of get_16x16? or the statistics for a run of bitmap_to_16x16 relate to the statistics for set_16x16; etc.)

Submit this as a PDF document named a4-part-5.pdf. It must be no shorter than one page and no longer than two pages.

What you must submit

• Your completed work in the four assembly files: a4-part-1.asm, a4-part-

2.asm, a4-part-3.asm, and a4-part-4.asm.

• The PDF document named a4-part-5.pdf.

Evaluation

• 4 marks: Solution part • 5 marks: Solution part 2.
• 3 marks: Solution part • 5 marks: Solution part 4.
• 3 marks: Solution part