CPSC 2190 M01

(6 points) Consider the affine cipher with encryption function f(x) = (7x+5) mod 26. The decryption function is d(y) = (ay +b) mod 26, for a,b ∈ Z26. Find a and b. Recall that Zn = {`0,1,2,·· ,n − 2,n − 1`}.
Consider the following statements, where a,b,m ∈ Z and m >

a ≡ b (mod m) =⇒ a ≡ b (mod 2m)	(1)
a ≡ b (mod 2m) =⇒ a ≡ b (mod m)	(2)

(a) (3 points) Is statement (1) true or false? Prove or disprove it. (b) (3 points) Is statement (2) true or false? Prove or disprove it.

(4 points) Use Fermat’s little theorem to compute 7²⁰¹⁹(mod 11).
(4 points) Let f(x) = 10x²+ 2x + 4. Show that f(x) is O(x²), using the definition of

O(·).

(4 points) Let A,B be square matrices with elements in R. Prove by mathematical induction that if AB = BA then AⁿB = BAⁿfor all n ∈ N.
(a) (3 points) Use the Euclidean algorithm to find the gcd of 132 and 90.
- (3 points) Use your above work to find s,t ∈ Z such that gcd(132,90) = 132s+90t.
- (2 points) Did you find an inverse of 90 modulo 132? If so, what is the inverse? If not, why not?
(a) (4 points) Use back substitution to find the inverse of 23 modulo 31 in Z31.
- (2 points) Find a solution in Z31 to the linear congruence 23x ≡ 5 (mod 31).
(6 points) There are certain things whose number is unknown. If we count them by twos, we have one left over; by threes, we have one left over; and by fives, four are left over; by sevens, zero are left over. How many things are there? Find the smallest positive integer that satisfies this condition.
(6 points) In mathematics, the n-th harmonic number is the sum of the reciprocals of the first n natural numbers:

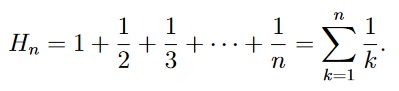
Use mathematical induction to prove that

H₁+ H₂+ ··· + H_n= (n + 1)H_n− n.