Computer Programming 143 Project

A research project at E&E Engineering provides remote monitoring and control of electric water heaters (EWHs), which are colloquially called geysers in South Africa. The focus of the work is efficient schedule control to save energy, and reporting to inform users to reduce water and energy consumption. For this project you will write an EWH

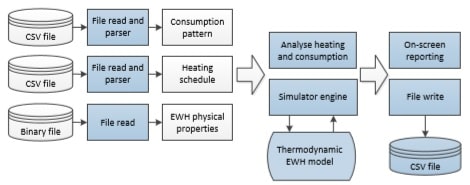
simulator that implements a simplified thermodynamic model. The main inputs into your simulator will be a consumption pattern, a heating schedule, and the EWH physical properties. The output from your simulator will be the electrical energy put into the EWH by the element, the thermal energy extracted from the EWH through water consumed, the volume of water used, and a breakdown and analysis of consumption (e.g. cost of a bath or shower). In part 1 you will write the code to: analyse given water consumption patterns to detect the beginning and end of events; analyse the heating schedule; and implement the thermodynamic model for the EWH to estimate the energy transfers and temperature changes for one simulation iteration. In part 2 you will write code to: read the consumption pattern, heating schedule, and physical properties from files; run the simulation over a whole day; and report the energy and cost per event and per day; and sort the events per cost. Part3 is more difficult, and not required to pass the project. Part 3 requires various extensions and analyses, and reporting into a file.

Instructions

1. All assignments for this practical must be submitted on SUNLearn.
2. Submit only your files that have the extension .c and .h
3. You may use multiple files, or put all your functions in one file.
4. You must do all parts of the project onyourown. If you are found to have copied any part of the project from any other source, unless instructed to do so in the instructions, the whole assignment will be considered incomplete. Copying can lead to suspension from the university.
5. You can use the same project for all three parts of the project.
6. Include a comment block at the top of each source file. It must include the correct filename and date, your name and student number, and the copying declaration.
7. Some of the questions have to be completed and demonstrated successfully to pass the project. Others are required to get more than 50%, and others are required to get more than or equal to 75%. They are clearly indicated in the instructions, and summarised below.
8. You will have to demonstrate your project and answer random questions on the project at the last practical session. Your mark for the project will partially be based on which sections you successfully completed, and your answers. The table below gives an indication of which sections you need to complete to pass the project. However, successful completion of each is a necessary but not sufficient condition – you will also have to answer questions during the demonstration. The list is provided to help you focus your attention.
9. Submit your code (.c files and .h files) by the deadline on SUNLearn. You have to atleast submit the code required to get 50%. The code must be submitted by the end of the relevant group’s practical session, as indicated on SUNLearn.
10. Your code must be demonstrated on an electronic classroom PC (S203/S207A/S207B), so be sure to test it on the electronic classroom PCs before demo day if you developed on your own computer.
11. 11. A lot of thought has gone into the definition of this project to ensure that you learn something from it. Be sure to use this opportunity to learn and ... enjoy!

1 Part 1

1.1 Goals

• Write code to analyse a hard-coded raw heating schedule to report the on/off times in that schedule
• Write code to analyse a hard-coded raw consumption pattern to report events in that pattern
• Implement a thermodynamic model to calculate energy transfers and resulting temperature changes for one simulation iteration

1.2 Background

You will be using a simple one-node model to model the EWH, which assumes that all water that enters the EWH through the inlet mixes immediately with the rest of the body of water, and that all the energy from the heating element immediately diffuses into the whole body of water.

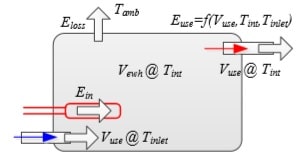
Figure 1: One-node model energy flows. Energy enters the EWH through the heating element, and leaves the EWH through standing losses and usage losses.

Figure 1 shows a so-called one-node representation of the energy flows present in an EWH. The temperatures used are the ambient temperature of the air around the EWH

(T_amb), the cold water temperature at the intlet (T_inlet), and the internal temperature of the water inside the EWH, which is also the temperature of the hot water leaving the

EWH (T_int).

Energy enters the EWH through the heating element, and is denoted by E_in. Energy leaves the EWH in two ways: (1) through standing losses, where energy is lost to the environment (E_loss), and (2) through the energy lost by replacing hot water that is drawn with cold water (E_use).

For these energy flows, we will use the following equation that states that the energy (in Wh) required to change the temperature of a body of water is equal to

E = cρV ∆T

Where: c is the specific heat capacity of water (Wh/(kg.K)); ρ is the density of water (kg/l); V is the volume (l), and ∆T is the change in temperature in degrees Kelvin. Since

1.2 Background

Kelvin is just a constant offset from Celsius, a change in temperature is the same in Kelvin as in Celsius. c is given as 4185.5J/(kg.K) – you have to convert it to Wh/(kg.K). Since the density of water is 1kg/l, equation 1 reduces to

E = cV ∆T (2)

1.2.1 Heating energy

Electrical energy is converted into thermal energy by the element, and this thermal energy is transferred at a rate that depends on the power rating of the element. For example, a 3kW = 3000W element transfers energy at a rate of 3000Wh of energy per hour, or 50Wh per minute.

However, the EWH also uses a thermostat with a “temperature set point ” (T_sp) to which the temperature in the EWH is controlled. The effect is that the element only turns on when the temperature of the water is below the set point. Assuming that the time over which the calculation is performed is short (i.e. that the thermostat will stay either on or off for the full duration), the energy transferred to the water (in Wh) over time ∆t is

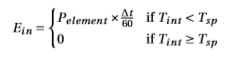
where P_element is the element power rating in W ; and ∆t is the duration over which the calculation is performed inminutes.

1.2.2 Usage losses

The balance of energy lost through a usage (or withdrawal) event (e.g. a bath or shower) is the difference of energy in the warm outlet water and in the the cold inlet. Put differently, the energy lost is the energy required to reheat the cold water to the same temperature as the volume of warm water that was used. The energy loss through usage over a sample interval is given by

E_use = cV_use(T_int −T_inlet) (4)

where E_use is the energy in Wh, V_use is the volume used in litres, and the difference in temperatures in degrees Kelvin or Celsius.

1.2.3 Standing losses

Standing losses refer to the energy lost due to heat dissipation from the water inside the EWH to the outside environment as a result of the temperature difference. Standing losses can be modelled as a first order differential equation that describes the temperature decay toward the ambient temperature:

dT_int/dt = −AG/cV_ewh(T_int−T_amb) (5)

Where: T_int is the temperature of the water in the EWH in degrees Kelvin; A is the surface area of the EWH that is exposed to the environment; G is the thermal conductivity of the EWH tank in W /(Km²); and T_amb is the temperature of the outside environment.

Assuming that no hot water usage losses and no heating occur, but only standing losses, solving Equation 5 results in the energy lost to the environment (E_loss) during this time:

E_loss =c V_ewh(T_int−T_amb)(1−e^α) (6)

where, for a duration ∆t inminutes,

α = ∆t/60 × −AG/cV_ewh (7)

1.2.4 Change in temperature

The balance of energy transferred from the heating element into the EWH’s water, the energy lost due to usage, and the energy lost due to standing losses have a combined resultant change in internal temperature in Kelvin or Celsius. It can be assumed that the combined temperature change is given by (valid for any time period)

∆T = E_in − E_use − E_loss/ cV_ewh (8)

1.3 Given information

You will find the following on learn.sun.ac.za to use in this part of the project.

• A header file called h is given, which contains a few heating schedule definitions. A heating shedule is an array of type heatingScheduleType (defined in the same file) with 1440 elements that gives an off or on status for each minute of the day. Note: This indicates whether electricity is supplied to the EWH for the time instant.
• A header file called h is given, which contains a few consumption pattern definitions. A consumption pattern is an array of type int with 1440 elements that gives the volume of water used in litres (as an integer) for each minute of the day.
• You can use the schedules and patterns as indicated in the example below if the appropriate .h files are included:

heatingScheduleType activeSchedule [24*60] = heatingScheduleTypicalValues; int activePattern [24*60] = consumptionPatternValues1;

1.4 Instructions

Implement the following for Part 1 of the project.

1.4.1 Time conversion

The indices of the heating schedule and consumption pattern arrays essentially represent the 24×60 = 1440 minutes of the day, ranging from 0 to 1439. For example, minute of the day 65 relates to hour of the day 1 and minute of the hour 5, i.e. 01:05. Write a function(s) to determine the hour of the day and minute of the hour to make the minute of the day human readable, i.e. to be able to convert 65 and print it out as 01:05. Hint: To add a leading zero to a single digit number, print it out as printf("%02d",n);

1.4 Instructions

1.4.2 Heating schedule analysis

Write a function that receives a reference to a heating schedule array and prints out the start and end times of each on heating period. The index of the array element represents the minute of the day. You will have to convert it to hour of the day and minute of day to make it human readable. Use the following prototype:

void printHeatingSchedule(heatingScheduleType * schedule);

1.4.3 Consumption pattern analysis

Write a function that receives a reference to a consumption pattern array and prints out the following for each consumption event:

• start and end times of consumption events
• volume of water per consumption event
• total volume consumed over the entire consumption pattern

Use the following prototype:

void printConsumptionPattern(int * pattern);

1.4.4 EWH Structure

Define a structure for the EWH variable with the following members, which will contain the physical properties of an EWH, and define a variable type alias of this structure called geyserType.

{`
struct geyserStruct { 
double thermalConductance; // G in W/(K.m^2) 
double internalTemperature;//in degC, 
initial value (updated by simulator) 
double setTemp; //Thermostat set temp in degC 
int volume; //in litres (meter can only measure whole litres) 
int elementRating; //in Watts 
double length; // length of EWH in meters 
double radius; // radius of EWH in metres 
double surfaceArea; //Area exposed to the environment in m^2 };
`}

1.4.5 Simulator

Write a function that performs one simulation step of the EWH, and has at least the following arguments:

• a reference to the EWH struct variable of the type defined in Section 1.4.4
• duration over which to perform simulation iteration inminutes
• temperature of cold water at the inlet for this iteration in ◦C
• ambient temperature of air around the EWH in ◦C
• volume of water used during the simulation iteration
• heating schedule setting (on or off ) of type heatingScheduleType

1.5nbsp; Verification

The function must return the electrical energy consumed by the element, E_in, in Wh. The function must calculate the electrical energy put in by the element (taking the thermostat in equation 3 into account), energy lost through use and energy lost through standing losses using the process described in section 1.2, and update the internal temperature based on the nett energy change.

1.5 Verification

Define the following preprocessor directives

{`
#define inletT 18 
#define ambientT 20 
#define c ____ //Wh/(kg.K) -- converted from 4185.5 Joule/(kg.K) 
`}

In the main function declare an EWH and assign values as follows:

{`
geyserType geyser; 
geyser.thermalConductance = 1.429756; //W/(K.m^2) 
geyser.volume = 150; 
geyser.elementRating = 3000; 
geyser.internalTemperature = 50; //initially starts warm 
geyser.setTemp = 65; 
geyser.length = 1.0; geyser.radius = 0.219; 
geyser.surfaceArea = geyser.length*2*M_PI*geyser.radius + 2*M_PI* pow(geyser. radius,2); //include math.h
`}

Verification - use the following to verify the pattern and schedule analysis.

{`
Testcode: 
heatingScheduleType heatingSchedule[] = heatingScheduleTypicalValues; //from heatingSchedules.h printHeatingSchedule (heatingSchedule); 
Output: 
Printing heating schedule 
On from 03:00 to 05:30 
On from 16:00 to 18:29 
On from 22:00 to 23:54
`}

{`
Testcode: 
int consumptionPattern [] = consumptionPatternValues1; //from controlPatterns.h printConsumptionPattern (consumptionPattern); 
Output: 
Printing consumption pattern 
Event from 00:08 to 00:09, volume = 4 litres 
Event from 05:30 to 05:33, volume = 65 litres 
Event from 07:38 to 07:38, volume = 2 litres 
Event from 10:11 to 10:13, volume = 35 litres 
Event from 17:30 to 17:34, volume = 49 litres 
Total volume consumed for the day 155 litres
`}

Verification - use the following examples to check that your simulation is working.

Note: the simulation time step is only forced to 60 minutes (an hour, in stead of one minute)here to have large renergy impacts and still be able to isolate different energy types. For the actual simulation runs, you will use one-minute simulation steps.

{`
Testcode:
printf("Alpha %f\n", alpha); //for duration of 60 minutes.
Alpha -0.013752
`}

{`
Testcode:
// ONLY standing losses, over 1 hour 
geyser.internalTemperature = 50; //reset internal temperature 
printf("%.2f; ", runSimulationStep(&geyser, 60, inletT, ambientT, 0, off)); 
printf("%.2f\n", geyser.internalTemperature);
Output: 0.00; 49.59 
(Eloss =71.4543,Euse =0)     
`}

{`
Testcode:
//ONLY heating and standing losses, over 1 hour 
geyser.internalTemperature = 50; //reset internal temperature 
printf("%.2f; ", runSimulationStep(&geyser, 60, inletT, ambientT, 0, on)); 
printf("%.2f\n", geyser.internalTemperature);
Ouput: 3000.00; 66.79 
(Eloss =71.4543,Euse =0)
`}

{`
Testcode:
//test thermostat temperature limit 
geyser.internalTemperature = 65; //set internal temperature to thermostat max 
printf("%.2f; ", runSimulationStep(&geyser, 60, inletT, ambientT, 0, on));
printf("%.2f\n", geyser.internalTemperature);
Ouput: 0.00 64.39 
(Eloss =107.1814,Euse =0) 
`}

{`
Testcode:
//with consumption, zero input, with standing losses, over 1 hour 
geyser.internalTemperature = 50; 
printf("%.2f; ", runSimulationStep(&geyser, 60, inletT, ambientT, 100, off)); 
printf("%.2f\n", geyser.internalTemperature);
Ouput: 0.00; 28.26 
(Eloss =71.4543,Euse =3720.44)
`}

{`
Testcode:
//with consumption, with input, with standing losses 
geyser.internalTemperature = 50; //reset internal temperature 
printf("%.2f; ",runSimulationStep(&geyser, 60, inletT, ambientT, 100, on)); 
printf("%.2f\n", geyser.internalTemperature);
Ouput: 3000.00; 45.46 
(Eloss =71.4543,Euse =3720.44)
`}

Part 2

2.1 Goals

• Read a heating schedule from a text file into an array.
• Read a consumption pattern from a text file into an array.
• Read physical EWH properties from a binary file
• Use the thermodynamic model from Part 1 to calculate the total electrical energy consumed for a heating schedule and consumption pattern.
• Analyse consumption per event.

2.2 Background

2.2.1 CSV files

Comma Separated Value (CSV) files are text files that contain values, separated by commas. CSV files are usually used to save large amounts of data in an easily transportable and viewable format – they can easily be opened in Excel, Matlab, Python, etc. You can open the given CSV files in Excel on most PCs by double-clicking the CSV file from Explorer. Note that the first row of a CSV file usually contains the column headings. You will therefore have to read and discard the first line before reading data.

2.2.2 Volume per event

The volume used per event i is the sum of the volumes over the duration of the event, and is given by

Where n_b is the first minute of the event, and n_e the last. Note: The usage energy lost per minute must use the internal temperature at the beginning of the minute, i.e. before the temperature change through the minute is calculated with the simulator.

2.3 Given

You will find the following on learn.sun.ac.za to use in this part of the project.

• Files named HeatingScheduleXX.csv that contain heating schedules. In the CSV files, an on is stored as a 1 and off as 0.

2.4 Instructions

• Files named csv that contain consumption patterns.
• Binary files named bin that contain geyser physical properties in the structure from section 1.4.4.
• A file called c and matching header file that contain a function that split a CSV string srcCSV into constituent strings str1 and str2. The function prototype is int parseCSV(char * srcCSV, char* str1, char* str2);

2.4 Instructions

2.4.1 Heating schedule from file

Write a function to open a heating schedule file (prompt the user for the filename) and read the values into the heating schedule array. Use the function written in Part 1 to display the loaded heating schedule.

2.4.2 Consumption pattern from file

Write a function to open a consumption pattern file (prompt the user for the filename) and read the values into the consumption pattern array. Note: The file only contains the minutes when water was flowing, while the minutes when no water was flowing are omitted. So, when the consumption pattern is read into the array, you will have to fill in the zeros. Use the function written in Part 1 to display the summary of the loaded consumption pattern.

2.4.3 EWH Physical properties from file

Write a function to read the physical properties of the EWH from a file – prompt the user for the filename. Read the values into your variable of type geyserType and display the read values. The file is 56 bytes long, and matches the structure from section 1.4.4. Use the sizeof function when reading from the file to read the whole structure variable in one step. If your system represents the same structure in more than 56 bytes, you will have to read the members individually.

2.4.4 Energy analysis

Write a function to use the loaded heating schedule, loaded consumption pattern, loaded physical properties, and the simulator written in part 1 of this project to determine and display the following:

• Event information
  • Start time and duration
  • Volume of water
  • Thermal energy (E_use) and cost thereof (assume R50/kWh)
  • Average temperature (use the temperature at the beginning of the minute)
• Daily information

2.5 Verification

• Volume of water
• Electrical energy put in and cost thereof
• Thermal energy used per day and cost thereof.

2.5 Verification

The files named HeatingSchedule00.csv, ConsumptionPattern.csv, and GeyserPhysical00

.bin contain the same information as that in Part 1 of the project. Use the following for verification:

{`
Output: For HeatingSchedule00.csv
Printing heating schedule
On from 03:00 to 05:30
On from 16:00 to 18:29
On from 22:00 to 23:54
`}

{`
Output: For ControlPattern00.csv
Printing consumption pattern
Event from 00:08 to	00:09, volume = 4 litres
Event from 05:30 to	05:33, volume = 65 litres Event from 07:38 to	07:38, volume = 2 litres
Event from 10:11 to	10:13, volume = 35 litres
Event from 17:30 to	17:34, volume = 49 litres
Total volume consumed for the day 155 litres
`}

{`
Output: For Physical00.bin
Printing geyser physical properties
Thermal conductance: 1.429756 W/(K.m^2)
Internal temperature: 50.000000 degC
Set temperature: 65.000000 degC
Volume: 150
Element rating: 3000 Watts
Length: 1.000000 m
Radius: 0.219000 m
`}

{`
Output: For the the heating schedule, the consumption pattern, and the physical properties
Start Duration Volume Energy Cost Ave Temp time min litres kWh Rand degC
===========================================================
00:08	2	4	0.148	0.22	49.8
05:30	4	65	3.050	4.58	59.5
07:38	1	2	0.067	0.10	46.9
10:11	3	35	1.049	1.57	43.2
17:30	5	49	2.303	3.46	59.0
Total energy put in	= 11.050 kWh (R 16.57),
Total energy extracted = 6.617 kWh (R 9.93),
Total volume used	= 155 litres
`}

3.1 Instructions

Part 3

3.1 Instructions

This part of the project is more difficult and intended as suggestions for the student who would like toget 75%andmore for the project. The problems are purposely vaguely specified and it is left to the student to fill in the voids.

• Add the cost of water to the cost calculations.
• Sort the events according to cost (descending order) to highlight the more expensive events.
• Plot the events on a horizontal bar graph, using one asterisk per 100 Wh.
• Allow the user to create usage profiles and heating schedules through a user friendly interface where the user is only requested to enter start times, end times, and volume of water.
• Write the programme output to a CSV file that will allow analysis of the results in Excel.
• Modify the code to quantify and tabulate the impact on electrical input energy and resulting energy per event for each the following individually for a normally "on" heating schedule and consumption pattern:
  • 5% reduction in consumption volume
  • 5% increase in inlet temperature
  • 5%reduction in thermal conductance (improvement of resistance, for example with a blanket)
  • 5% rise in ambient temperature
  • 5% change in set temperature
  • suboptimal heating control (e.g. heating from three hours before until 30 minutes after use)
  • intelligent schedule control (heating from three hours before until at least 30 minutes before use)
• Determine (e.g. through brute force) the optimal heating schedule to guarantee hot water (> 48◦C) for each event in a consumption pattern.