Question 1—Generate and Count Passwords [10 marks]

Description

Using arrays, write a program that generates all possible 5 letter passwords containing only lowercase letters, uppercase letters, and/or digits. For example, “rot13” would be such a password, but “32RAx” would not because it has a hyphen. There are 62 letters to use (26 + 26 + 10). There are 62⁵ = 916132832 (almost a billion) possible passwords.

Test each password you generate to determine if it satisfies the following rules:

• At least one lowercase letter;
• At least one uppercase letter;
• At least one digit;
• No character can appear twice in a row (e.g. “Haax5” is not valid, but “Ha5ax” is).

Theory+

A list comprehension can have nested for loops. For example, the following list comprehension generates all possible passwords with letters that come from the string LETTERS. It has been formatted to emphasize the similarity to nested for loops, but notice there are no colons.

{`
passwords(=[ "".join([c0,(c1,(c2,(c3,(c4])
for c0 in LETTERS
for c1 in LETTERS
for c2 in LETTERS
for c3 in LETTERS
for c4 in LETTERS]
`}

If LETTERS is the string “0Aa”, the 243-entry result is:

{`
['00000','0000A','0000a','000A0','000AA','000Aa','000a0','000aA','000aa',
'00A00','00A0A','00A0a','00AA0','00AAA','00AAa','00Aa0','00AaA','00Aaa',
'00a00','00a0A','00a0a','00aA0','00aAA','00aAa','00aa0','00aaA','00aaa',
'0A000','0A00A','0A00a','0A0A0','0A0AA','0A0Aa','0A0a0','0A0aA','0A0aa', 
'0AA00','0AA0A','0AA0a','0AAA0','0AAAA','0AAAa','0AAa0','0AAaA','0AAaa',
'0Aa00','0Aa0A','0Aa0a','0AaA0','0AaAA','0AaAa','0Aaa0','0AaaA','0Aaaa',
'0a000','0a00A','0a00a','0a0A0','0a0AA','0a0Aa','0a0a0','0a0aA','0a0aa', 
'0aA00','0aA0A','0aA0a','0aAA0','0aAAA','0aAAa','0aAa0','0aAaA','0aAaa',
'0aa00','0aa0A','0aa0a','0aaA0','0aaAA','0aaAa','0aaa0','0aaaA','0aaaa',
'A0000','A000A','A000a','A00A0','A00AA','A00Aa','A00a0','A00aA','A00aa', 
'A0A00','A0A0A','A0A0a','A0AA0','A0AAA','A0AAa','A0Aa0','A0AaA','A0Aaa',
'A0a00','A0a0A','A0a0a','A0aA0','A0aAA','A0aAa','A0aa0','A0aaA','A0aaa',
'AA000','AA00A','AA00a','AA0A0','AA0AA','AA0Aa','AA0a0','AA0aA','AA0aa', 
'AAA00','AAA0A','AAA0a','AAAA0','AAAAA','AAAAa','AAAa0','AAAaA','AAAaa',
'AAa00','AAa0A','AAa0a','AAaA0','AAaAA','AAaAa','AAaa0','AAaaA','AAaaa',
'Aa000','Aa00A','Aa00a','Aa0A0','Aa0AA','Aa0Aa','Aa0a0','Aa0aA','Aa0aa', 
'AaA00','AaA0A','AaA0a','AaAA0','AaAAA','AaAAa','AaAa0','AaAaA','AaAaa',
'Aaa00','Aaa0A','Aaa0a','AaaA0','AaaAA','AaaAa','Aaaa0','AaaaA','Aaaaa', 
'a0000','a000A','a000a','a00A0','a00AA','a00Aa','a00a0','a00aA','a00aa',
'a0A00','a0A0A','a0A0a','a0AA0','a0AAA','a0AAa','a0Aa0','a0AaA','a0Aaa',
'a0a00','a0a0A','a0a0a','a0aA0','a0aAA','a0aAa','a0aa0','a0aaA','a0aaa', 
'aA000','aA00A','aA00a','aA0A0','aA0AA','aA0Aa','aA0a0','aA0aA','aA0aa',
'aAA00','aAA0A','aAA0a','aAAA0','aAAAA','aAAAa','aAAa0','aAAaA','aAAaa',
'aAa00','aAa0A','aAa0a','aAaA0','aAaAA','aAaAa','aAaa0','aAaaA','aAaaa', 
'aa000','aa00A','aa00a','aa0A0','aa0AA','aa0Aa','aa0a0','aa0aA','aa0aa',
'aaA00','aaA0A','aaA0a','aaAA0','aaAAA','aaAAa','aaAa0','aaAaA','aaAaa',
'aaa00','aaa0A','aaa0a','aaaA0','aaaAA','aaaAa','aaaa0','aaaaA','aaaaa']
`}

If we wanted the locations of each letter in LETTERS instead, we could write

{`
passwords = [c0,c1, c2, c3, c4)
for c0 in range (len LETTERS))
for c1 in range (len LETTERS))
for c2 in range (len LETTERS))
for c3 in range (len LETTERS))
for c4 in range (len LETTERS))
`}

which yields

{`[(0, 0, 0, 0, 0), (0, 0, 0, 0, 1), (0, 0, 0, 0, 2), (0, 0, 0, 1, 0), (0, 0, 0, 1, 1), (0, 0, 0, 1, 2), (0, 0, 0, 2, 0), (0, 0, 0, 2, 1), (0, 0, 0, 2, 2), (0, 2, 0, 0, 0),
…
(2, 2, 2, 0, 1), (2, 2, 2, 0, 2), (2, 2, 2, 1, 0), (2, 2, 2, 1, 1), (2, 2, 2, 1, 2), (2, 2, 2, 2, 0), (2, 2, 2, 2, 1), (2, 2, 2, 2, 2), 
`}

This code is a good example of the flexibility of Python, but it is not good for tackling really big problems, because the storage scheme wastes space, and the interpreted code is relatively slow (although this code is faster than most because it is so short). If we generate the last list of tuples as a 2Rdimensional numpy array, however, we can shrink the storage, and increase the speed of operations on this data structure by an order of magnitude, so we can tackle larger problems.1

In fact, since all the numbers in this data structure are small, we can pick a data type that reduces the size even more. We will be considering LETTERS containing all digits, all lowercase letters and all uppercase letters, with a total of 10 + 26 + 26 = 62 characters, so the numpy.int8 data type, which is an 8Rbit (1 byte) integer representing numbers from R128 to 127, will work fine and save us lots of space. Storing one million of these numbers requires only 1 MB of memory, in comparison with the 8 MB of memory needed to store the same numbers using the default 64Rbit ints.

The list of tuples shown above looks like the text box to the right as an array. To generate this array, first make an array of the right size and type with np.zeros((numRows, numCols), dtype=np.int8). Then fill each column. Each column consists of the digits from 0 to nR1 in order, where n is the length of LETTERS, in this case 3. Each number is repeated 1 time in the last column, n times in the second last column, n2 times in the third last column, etc. Then the whole sequence from 0 to nR1 is repeated as many times as necessary to fill the column length of n5. You can use np.arange to generate the sequence of numbers, np.repeat to create repetitions of each entry, and np.resize to cause an entire array to repeat as many times as necessary to fill a designated size.

Once you have an array, do all your operations on the entire array, or on entire columns of the array. For example, to find if there are entries in the 0 column that are equal to entries in the1 column, use array[:,0] == array[:,1], which yields a boolean array of the same length as a column. What would np.sum[:,0] == array[:,1]) represent?

What to do

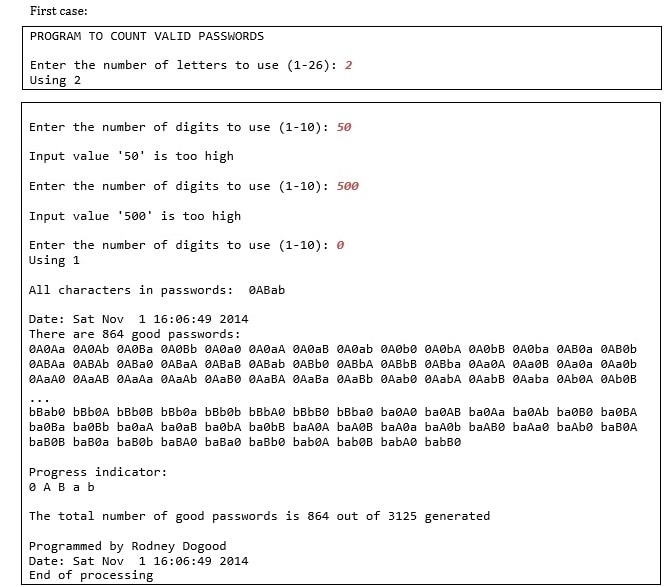
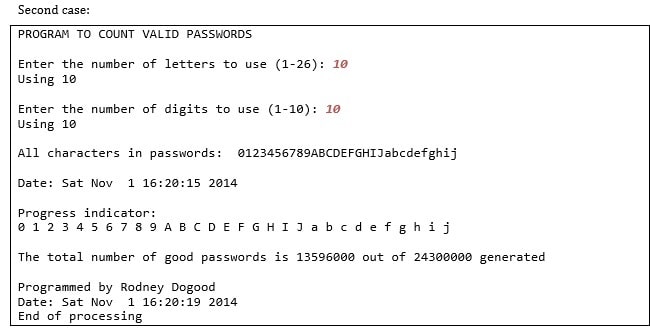
Write a complete script file that prompts the user to specify how many letters of the alphabet, from 1 to 26, and how many digits, from 1 to 10, are to be used. It should then generate all 5Rcharacter passwords using just those letters (both upper and lower case) and digits. It should test each candidate against the rules stated in the Description section, and count the number of passwords that pass the test.

Details:

Sample Output