Probability distributions Assignment Help
A wine dealer has classified the last 200 customers according to the criteria given in the table below. Determine whether buying American wine and being 50 and over are independent events.
| Type of Wine | Less than 30 years old | Between 30 and 50 years old | 50 years old and over | Total |
|---|---|---|---|---|
| American | 100 | 30 | 20 | 150 |
| French | 2 | 2 | 16 | 20 |
| German | 2 | 16 | 2 | 20 |
| Other | 4 | 6 | 0 | 10 |
| Total | 108 | 54 | 38 | 200 |
Probability distributions Assignment Help By Online Tutoring and Guided Sessions from AssignmentHelp.Net
Probability of A = Probability of people buying American wines = 150/200
Probability of B = Probability of customers being 50 and above 50 years = 38/200
Probability of ( A and B ) = Probability of people who are buying American wines and being 50 years age or more than 50 = 20/200
For A and B to be independent P(A)*P(B) = P(A and B)
These are not independent events, since they do not satisfy this property
Since P(A)*P(B)= 38/200 * 150/200 which is not equal to P(A and B) = 20/200
For the next three years, depending on market conditions, a firm may make either a profit of £80 million or a loss of £20 million each year. (The outcome each year is independent of the outcome in other years.) Each year the probability of making a profit is ¾. If T is the total profit/loss in the three years, find the probability distribution for T.
| Profit in Year 1 | Profit in year 2 | Profit in year 3 | Total Profit in 3 years | Probability |
|---|---|---|---|---|
| 80 | 80 | 80 | 240 | ¾*3/4*3/4 = 27/64 |
| 80 | 80 | -20 | 140 | ¾*3/4*1/4 = 9/64 |
| 80 | -20 | 80 | 140 | 9/64 |
| -20 | 80 | 80 | 140 | 9/64 |
| -20 | -20 | 80 | 40 | ¾*1/4*1/4= 3/64 |
| 80 | -20 | -20 | 40 | 3/64 |
| -20 | 80 | -20 | 40 | 3/64 |
| -20 | -20 | -20 | -60 | 1/64 |
Then the probability distribution of total profit in three years is given by:
| T (= total profit) | P(T) |
|---|---|
| 240 | 27/64 |
| 140 | 9/64 |
| 40 | 3/64 |
| -60 | 1/64 |
A store is about to place an order for the expected number of microwave ovens demanded, based on the probability distribution in the table below.
| NUMBER DEMANDED | PROBABILITY |
|---|---|
| 0 | 0.05 |
| 1 | 0.10 |
| 2 | 0.20 |
| 3 | 0.30 |
| 4 | 0.20 |
| 5 | 0.10 |
| 6 | 0.05 |
EXPECTED NUMBER OF MICROWAVE OVEN = Ʃ x*p(x) WHERE x = NO. OF MICROWAVE DEMANDED.
= 0*0.05 + 1*0.10 + 2*0.20 + 3*0.30 + 4* 0.20 + 5*0.10 + 6*0.05
= 3
Variance of x = Ʃx2*p(x) –Ʃ(x*p(x))2
=11.1-9=2.1
A national survey of married couples showed that 30% of the wives and 50% of the husbands watched a certain TV program. Also, if the wife watched, the probability that the husband watched increased to 60%. For a couple drawn at random, calculate the probability that: (a) the couple both watch (b) at least one watches (c) neither watches (d) if the husband watches, the wife watches (e) if the husband does not watch, the wife watches.
Given –
P(A) = 30/100 where A = Percentage of wives watching a TV programme
P(B) = 50/100 where B = Percentage of husbands watching a TV programme
P(B/A) = 60/100 where B/A is percentage of husband watching a TV programme given that wife has already watched it.
a) P(A and B) = ?
P(B/A) = P(A and B)/P(A)
So, P(A and B) = 60/100 * 30/100
= 1800/10000
= .18
b) P( at least one watches ) = P( A or B)
=P(A) + P(B) –P( A and B)
= 30/100 + 50/100 – 18/100
= 62/100
c) P (neither watches) = P(A’ and B’)
= 1- P(A or B)
= 1-62/100
= 38/100
d) P( husband watches, the wife watches) = P(B/A)
= P (A and B ) / P(A)
= 18/100 / 30/100
= 3/5
e) P( husband does not watch, wife watch ) = P(B’/A)
= P( B’ and A)/P(A)
= P ( A) –P(A and B ) /P (A)
= 30/100 – 18/100 / 30/100
= 2/5
Suppose that a firm’s total cost is given by C = 2 + 15Q, where Q is the firm’s output. The expected value and variance of output are known to be, respectively, E(Q) = 10 and V(Q) = 5. What are the expected value and variance of total cost?
C= 2+15Q
Given-
E(Q)= 10
E(C)= 2+15E(Q)
= 2+15*10
= 152
ALSO GIVEN-
VARIANCE (Q)
= 5
Variance (C) = 15*15*variance(Q)
= 15*15*5
= 1125
Show that Var(X) = E(X2) - [E(X)]2
By definition, Var(X) = E[(X-μ)2]
= E(X2 + μ2 - 2Xμ)
= E(X2)+E(μ2)- E(2Xμ)
Recall that µ = E(X) where µ = mean of random variable and E(aX) = aE(X)
= E(X2) + μ2 - 2μE(X)
= E(X2)+ μ2 - 2μ.μ
= E(X2) - μ2
= E(X2)- [E(X)]2
(Bayes’ theorem) Bag A contains 6 red and 4 yellow balls, while bag B contains 3 red and 7 yellow balls. A ball is drawn at random from one bag and turns out to be red. What is the probability that the ball came from bag A?
Probability of E1 = 1/2 where E1 = Probability of drawing ball from bag 1
Probability of E2 = 1/2 where E2 = Probability of drawing ball from bag 2
A = Drawing a Red ball
Probability of (A/E1) = 6/10 where A/E1 = drawing ball from 1 which is red in colour
Probability of (A/E2) = 3/10 where A/E2 = drawing ball from 2 which is red in colour
By Bayes Theorem
Probability of (E1/A) =
P(E1)*P(A/E1) / P(E1)*P(A/E1) + P(E2)*P(A/E2)
= ½*6/10 / ½*6/10 + ½*3/10
= 2/3
A thoroughly honest game-show host has placed a car behind one of three doors. There is a goat behind each of the other doors. You have no prior knowledge that allows you to distinguish among the doors. “First you point toward a door,” he says. “Then I’ll open one of the other doors to reveal a goat. After I’ve shown you the goat, you make your final choice whether to stick with your initial choice of doors, or to switch to the remaining door. You win whatever is behind the door.” In search of the car, you begin by pointing to door number 1. The host shows you that door number 3 has a goat. Does your chance of getting the car increase by switching your choice to door 2?
Chance of getting a car has increased whether you switch or not because earlier probability of getting a car is 1/3 , after pointing towards door 1, you came to know that door 3 has goat, now the probability of getting a car is ½ which means it has increased.
You are offered a chance to win £1000. All you have to do is throw 5 heads in a row when flipping a fair coin and pay the £20 entry fee. What is the probability of flipping 5 heads in a row? Will you play?
P(5 heads in a row) = 0.03125
Expected profit = (1000 – 20) * 0.03125 + (-20) * (1- 0.03125)
= 11.25
We will not play as the expected profit after winning is not greater than what we had paid.
A firm has n = 6 major customers and knows that each one has a probability p = 0.25 of calling on any day and that they call independently of one another. • What kind of distribution does X (the number of major customers that will call tomorrow) follow? • How many do you expect will call? • What is the probability that exactly 2 out of the 6 major customers will call?
- X follows binomial distribution because the trials are independent; that is, the outcome on one trial does not affect the outcome on other trials.
- Expectation of X = np
= 6*0.25
= 1.5 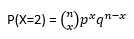
Here n = 6, p =0.25, q=0.75, x = 2
It implies P(X=2) = 0.05932
A sample of 5 voters is to be randomly drawn from the US population, when 60% vote Republican. a. The number of Republican voters in this sample of 5 can vary anywhere from 0 to 5. Tabulate its probability distribution. b. Calculate the mean and the standard deviation. c. What is the probability of getting exactly 3 Republican voters in the sample? d. Calculate the probability that the sample will have at least 3 Republican voters.
| X | P(X) | X*P(x) |
|---|---|---|
| 0 | 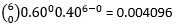 | 0 |
| 1 | 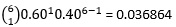 | 0.036864 |
| 2 | 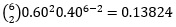 | 0.27648 |
| 3 | 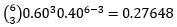 | 0.82944 |
| 4 | 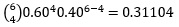 | 1.24416 |
| 5 | 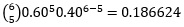 | 0.93312 |
b)
Expectation = Ʃ X*p(X) = 3.3200
Standard deviation = npq
= 6*0.60*0.40
= 1.44
c) Probability of x = 3
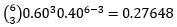
d) Probability of at least 3 republican voters = P(x≥3) = P(x=3) + P(x=4) + P(x=5) = 3.00672


