Graphs, Graphing Equations and Inequalities Assignment Help

Introduction to Graphs, Graphing Equations and Inequalities:
Graph:
A graph is depicted in diagrammatic form as asset of dots for the vertices joined by line or curve. It is a representation of set of object where some object are connected by the links. Vertices are the interconnected objects.
Types of graphs:
Distinction in terms of the main definition
- Undirected graph
- Directed graph
- Mixed graph
- Multi-graph
- Quiver
- Simple graph
- Weighted graph
- Half-edges, loose edges
Important graph classes
- Regular graph
- Complete graph
- Finite and infinite graphs
- Graph classes in terms of connectivity
- Category of all graphs
Graphing with slope-intercept:
y=(-1)/3 x+2
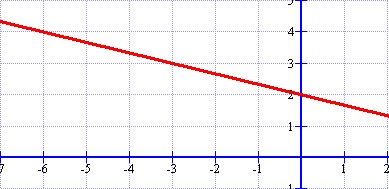
1. Start by graphing the y-intercept (b = 2).
2. From the y-intercept, apply rise over run using your slope. rise = 1, run = -3
3. Repeat this again from your new point.
4. Draw a line through your points.
Graphing Linear Inequalities:
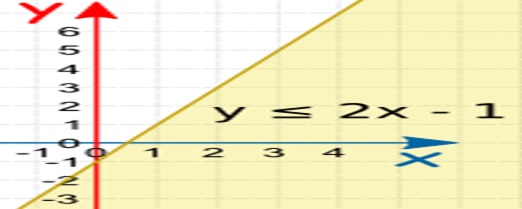
A Linear Inequality is like a Linear Equation (such as y = 2x+1), but it will have an Inequality like <, >, , or instead of an =.
How to Graph a Linear Inequality
First, graph the "equals" line, then shade in the correct area. There are three steps:
1. Rearrange the equation so "y" is on the left and everything else on the right.
2. Plot the "y=" line (make it a solid line for y or y, and a dashed line for y< or y>)
3. Shade above the line for a "greater than" (y> or y) or below the line for a "less than " (y< or y).
Example for inequality:
Equation: y 2x-1
The inequality already has "y" on the left and everything else on the right, so no need to rearrange Plot y=2x-1

Shade the area below (because y is less than or equal to)