Geometry Triangle Assignment

1. Find the measures of the following to the nearest tenth of a degree.

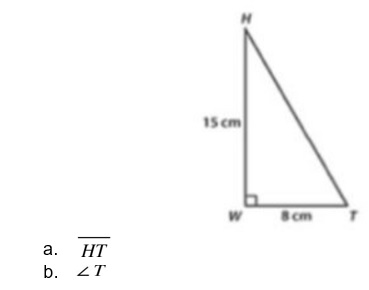
Solution

1. HT is the hypotenuse of a right angled triangle HWT thus we use Pythagoras theorem stating a² + b² = c² where c is the hypotenuse side thus Ht² = hw² +wt²

Ht² =15² + 8², HT² = 289, HT= √ (289), HT =17

1. Angle T we use cosine where cosine of angle T is adjacent side to this angle t divided by hypotenuse. Thus cos inverse of this value gives us value of <T

COS (T) = 8/17, <T = COS^-1 (8/17), <T cos-1(0.4706) = 61.9 ⁰

<T = 61.9 ⁰

2. What is the area of the given triangle?

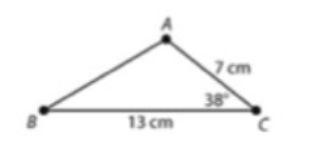
Solution

To calculate the area of the above triangle we will use the formula,

Area = ½ *a*b * sin (c) ,where a and b are any two given sides of the triangle and c is the angle between the two sides thus

Area = ½ *7*13* sin (38), 1/2*7cm*13cm*sin (38) = 28.0126 cm²

3. If X and Y are complementary angles sinX=15/17, and cosX=8/17, find each of the following :

1. tan X =

1. sin Y =

1. cos Y =

1. tsn Y =

Solution

First we put the given information into a diagram

We know Sin x = opposite side /hypotenuse side, cos x = adjacent side /hypotenuse

Thus this is a triangle with opposite side =15, adjacent side = 8 and hypotenuse =17

Also it’s a right angled triangle since 8² = 15² =17²=289

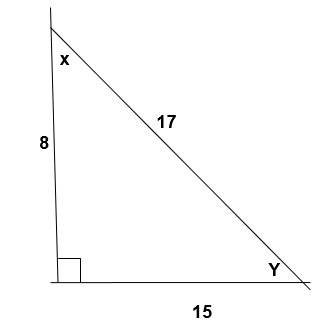
1. Tan x =opposite/ adjacent = 15/8 =1.875
2. Sin y = opposite/hypotenuse = 8/17 = 0.4706
3. Cos y= adjacent/ hypotenuse = 15/17 = 0.8824
4. Tan y = opposite/hypotenuse =8/15 = 0.5333