FIN4320 Exam 4
FIN 4320 – Exam 4
1. Dan bought some shares of a company at a total cost of $12,500 3 years ago. Today the value of these stocks is $17,800. If Dan donates all these shares to the charity, how much would be his cash savings from this tax strategy? Assume Dan is in 25% marginal tax bracket and long term capital gain tax rate is 15%.
$5,245
$12,500 x 15% = $1,875
$17,800 x 15% = $2,670
$2,670 - $1,875 = $795
$17,800 x 25% = $4,450
$4,450 + $795 = $5,245
2. Compute the difference between accumulated savings (net of taxes) for $15,500 (pretax) placed in bonds yielding 6.5% in a qualified pension versus an investment in a municipal bond yielding 3.5%. The municipal bond sum deposited was made with after-tax dollars on the same pretax amount. The marginal tax rate was 25%. Assume that the sums were accumulated for 25 years and the pension was liquidated at that time.
$28,650
Investment in a qualified pension:
Lump sum accumulated over 25 years:
N = 25
I/Y = 6.5%
PV = $15,500
PMT = 0
FV = $74,829.33
After-tax amount = $74,829.33 x (1-.25) = $56,122
Investment in a municipal bond:
Investment amount = $15,500 x (1-.25) = $11,625
Investment value in 25 years:
N = 25
I/Y = 3.5%
PV = $ 11,625
PMT = 0
FV = $27,472.72
After-tax amount = $27,472.72
$56,122 - $27,472.72 = $28,649 or $28,650
3. Jose, age 25, currently saves $13500 per year in his retirement account which is expected to earn 5% return. Jose is planning to retire at 62 and needs to fund his retirement upto age, 85. He has estimated that the annualamount needed during retirement would be $47,000 in today's dollar terms. The inflation rate is expected to be 1.5%. Calculate the shortfall (if any) in his retirement account at the beginning of retirement.
No Shortfall
Part A: Find the total amount which he needs in his retirement nest to fund rest of life.
Step 1: Compute the annual requirement at the beginning of the retirement
PV = $47,000
N = 62 – 25 = 37
I/Y = 1.5%
PMT = 0
FV = ? = $81,534.50 = $81,535
Step 2: Compute the real rate of return at which we need to find the present value of annual requirement of $81,534.50 during 62 – 85.
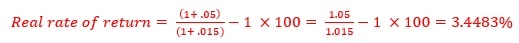
Step 3: Compute the PV of annual requirement at 3.4483% for 85 – 62 = 23 years
BGN MODE
FV = 0
N = 23
I/Y = 3.4483%
PMT = $81,535
PV = ? = $1,324,466.63 = $1,324,477
Part B: Calculate the additional savings if shortfall. Computer PMT. Use END MODE
PV = 0
PMT = $13,500
N = 37
I/Y = 5%
FV = $1,371,979.88 = $1,371,980
$1,371,980 - $1,324,477 = $47,503
No Shortfall
4. Jose, age 25, currently saves $13500 per year in his retirement account which is expected to earn 5% return. Jose is planning to retire at 62 and needs to fund his retirement upto age, 85. He has estimated that the annualamount needed during retirement would be $47,000 in today's dollar terms. The inflation rate is expected to be 1.5%. Calculate the lump sum amount required at the beginning of retirement to fund his post retirement period.
$1,324,251
Part A: Find the total amount which he needs in his retirement nest to fund rest of life.
Step 1: Compute the annual requirement at the beginning of the retirement
PV = $47,000
N = 62 – 25 = 37
I/Y = 1.5%
PMT = 0
FV = ? = $81,534.50 = $81,535
Step 2: Compute the real rate of return at which we need to find the present value of annual requirement of $81,535 during 62 – 85.
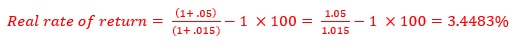
Step 3: Compute the PV of annual requirement at 3.45% for 85 – 62 = 23 years
BGN MODE
FV = 0
N = 23
I/Y = 3.45%
PMT = $81,535
PV = ? = $1,324,259 = $1,324,251???
5. Jose, age 25, currently saves $13500 per year in his retirement account which is expected to earn 5% return. Jose is planning to retire at 62 and needs to fund his retirement upto age, 85. He has estimated that the annual amount needed during retirement would be $47,000 in today's dollar terms. The inflation rate is expected to be 1.5%. Compute the additional annual savings (if needed) to fund the shortfall in retirement account (if any).
No additional savings are needed
Part A: Find the total amount which he needs in his retirement nest to fund rest of life.
Step 1: Compute the annual requirement at the beginning of the retirement
PV = $47,000
N = 62 – 25 = 37
I/Y = 1.5%
PMT = 0
FV = ? = $81,534.50 = $81,535
Step 2: Compute the real rate of return at which we need to find the present value of annual requirement of $81,534.50 during 62 – 85.
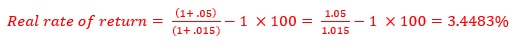
Step 3: Compute the PV of annual requirement at 3.4483% for 85 – 62 = 23 years
BGN MODE
FV = 0
N = 23
I/Y = 3.4483%
PMT = $81,535
PV = ? = $1,324,466.63 = $1,324,477
Part B: Calculate the additional savings if shortfall. Computer PMT. Use END MODE
PV = 0
PMT = $13,500
N = 37
I/Y = 5%
FV = $1,371,979.88 = $1,371,980
$1,371,980 - $1,324,477 = $47,503
No additional savings are needed
6. Frances bought a car for $44,500 as a business investment opportunity. She is allowed to depreciate over 10 years and take it as business tax deduction. At the end of the 6th year she sells this car for $22,000. Compute the cumulative cash benefit after sale on this transaction. Assume that Frances can earn 4.5% after tax returns and is in 25% tax bracket. Tax rate on gain is 15%.
$6,842.54
Step 1: Compute the cumulative tax benefit of depreciation for 10 years
Yearly Deductible Depreciation = $44,5000 ÷ 10 = $4,450
Yearly Tax Benefit = $4,450 x 25% = $1,125.50
N = 6
I/Y = 4.5%
PMT = $1,112.50
PV = 0
FV = ? = $7,472.54
Step 2: Compute the tax to be paid after 6 years on gain at the time of sale
Sale Price in the 6th year = $22,000
Depreciated Value of the car in the 6th year =$44,500 – ($4,450 x 6) = $17,800
Gain = $22,000 - $17,800 = $4,200
Tax on Gain = $4,200 x 15% = $630
Step 3: Compute Net Cash Earned (Step 1 – Step 2)
Cash Inflow = $7,472.54
Cash Outflow = $630
$7,472.54 - $630 = $6,842.54
Net Cash Earned = $6,842.54
7. John made $45,000 a year and had an annual investment cost of $250 and fees to a tax preparer of $525 per year. Each year John's total deduction fell short of the miscellaneous expenditure floor of 2% of AGI. He decides to cluster two years of his tax planning expenditure by visiting his tax planner twice in one year (i.e.,February for the past year and December for the next year.) How much would be deduction due to this clustering?
$400
$45,000 x 2% = $900
$250 + $525 +$525 = $1,300
$1,300 - $900 = $400
8. Richard and Sue wants to provide full funding for their 3 year old daughter who is expected to start college when she is 18. The current annual cost of a 4 year college is $38,000 which is expected to increase by 3.5% per year. They expect to earn 5% on their investment. They have already saved $8,000 in a college fund for this purpose. Calculate the additional amount they should save by the end of every year in order to accumulate funding for 4 years of college when their daughter turns 18.
$10,780
Step 1: Annual cost of education when the child starts college
PV = $38,000
N = 18 – 3 = 15
I/Y = 3.5%
PMT = 0
FV = ? = $63,663.26
Step 2: Total amount required (lump sum) at the beginning of 18th year
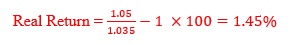
BGN MODE
PMT = $63,663.26
N = 4
I/Y = 1.45%
FV = 0
PV = ? = $249,245.34 = $249,245
Step 3: Additional savings
END MODE
FV = $249,245
I/Y = 5%
N = 15
PV = $8,000
PMT = $10,779.85 = $10,780
9. Richard and Mary wants to provide full funding for their 3 year old daughter who is expected to start college when she is 18. The current annual cost of a 4 year college is $38,000 which is expected to increase by 3.5% per year. They expect to earn 5% on their investment. Calculate the total cost (lump sum amount) required by them to fund 4 years of college when their daughter turns 18.
$249,245
Step 1: Annual cost of education when the child starts college
PV = $38,000
N = 18 – 3 = 15
I/Y = 3.5%
PMT = 0
FV = ? = $63,663.26
Step 2: Total amount required (lump sum) at the beginning of 18th year
BGN MODE
PMT = $63,663.26
N = 4
I/Y = 1.45%
FV = 0
PV = ? = $249,245.34 = $249,245
10. Susanna a businesswoman is in 33% tax bracket. She asks her clients to bill her in February of the following year instead of December of the current year. Her billing is for $22,000 per year. Compute the cumulative tax benefit of this deferral if she can earn 6.25% return on her investment and plans to repeat this process for the next 15 years.
$10,765
Yearly Tax Deferral = $22,000 x 33% = $7,260
Yearly Tax Benefit = $7,260 x 6.25% = $453.75
Cumulative Tax Benefit:
N = 15
I/Y = 6.25%
PMT = $453.75
PV = 0
FV = ? = $10,764.81 = $10,765
11. A client is concerned about the impact that inflation will have on her retirement income. The client currently earns $38,000 per year. Assuming that inflation averages 2.25% for the first five years, 2.5% for the next five years and 3.25% for the remaining time until retirement. What amount must her first-year retirement income be when she retires 13 years from now if she wants it to equal the purchasing power of her current earnings?
$52,892
After first 5 years:
PV = $38,000
N = 5
I/Y = 2.25%
PMT = 0
FV = ? = $42,471.75
After the next 5 years:
PV = $42,471.75
N = 5
I/Y = 2.5%
PMT = 0
FV = ? = $48,052.89
Remaining years (13th year):
PV = $48,052.89
N = 3
I/Y = 3.25%
PMT = 0
FV = $52,891.96 = $52,892
12. Sam and Sue wants to provide full funding for their 7 year old daughter who is expected to start college when she is 18. The current annual cost of a 4 year college is $38,000 which is expected to increase by 3.5% per year. Sam and Sue expect to earn 4.5% on their investment. Calculate how much they should save by the end of every year in order to accumulate funding for 4 years of college when their daughter turns 18.
$15,803
Step 1: Annual cost of education when the child starts college
PV = $38,000
N = 18 – 7 = 11
I/Y = 3.5%
PMT = 0
FV = ? = $55,478.85
Step 2: Total amount required (lump sum) at the beginning of 18th year

Real Return =
BGN MODE
PMT = $55,478.85
N = 4
I/Y = .97%
FV = 0
PV = ? = $218,737.98 = $218,738
Step 3: Additional savings
END MODE
FV = $218,738
I/Y = 4.5%
N = 11
PV = 0
PMT = $15,803.42 = $15,803
13. Jason, age 14, was given a choice of $80,000 to be deposited in his account today orhis parents would fund 80% of lump sum cost of 4 years of college. The first year of his college cost when he turns 18 is expected to amount to exactly $30,000 a year (i.e., in future dollar terms). Which should he take given a 7% after-tax investment return in both cases? Assume that the cost of education increases by 5% per year.
deposit, since its future value would be $104,864 while that of 80% of cost would be $91,597
Alternative 1: Funding 80% of college cost by parents
Step 1: Calculate the real rate (RR)
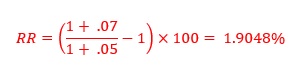
Step 2: The cost of college during the 1st year is $30,000. Calculate the total cost (lump sum) of 4 years of college as follows:
BGN MODE
N = 4
I/Y = 1.9048
PMT = $30,000
FV = 0
PV = ? = $116,677.18
Parents contribution = $116,677.18 x 80% = $93,341.74
Alternative 2: Depositing $80,000 today. Compute future value.
BGN MODE
PV = $80,000
I/Y = 7%
N = 4
PMT = 0
FV = $104,863.68 = $104,864
Depositing the $80,000 is the better option
14. Martha has estimated that she would need $35,000 per year (in today's $ terms) to live on in retirement. She will be retiring in 30 years and is funding for a 23-years retirement period. The inflation rate is expected to be 2% per year and the after-tax return on her investments is expected to be 5.5%. Calculate the annual amount she would need at the beginning of her retirement.
$63,398
Step 1: Annual amount she would need at the beginning of her retirement
PV = $35,000
N = 30
I/Y = 2%
PMT = 0
FV = ? = $63,697.66 = $63,398
15. Martha has estimated that she would need $35,000 per year (in today's $ terms) to live on in retirement. She will be retiring in 30 years and is funding for a 23-years retirement period. The inflation rate is expected to be 2% per year and the after-tax return on her investments is expected to be 5.5%. Calculate the lump sum amount required at the beginning of her retirement.
$1,031,578
Step 1: Cash shortfall at the beginning of retirement
PV = $35,000
N = 30
I/Y = 2%
PMT = 0
FV = ? = $63,697.66 = $63,398
Step 2: Lump sum needed at the beginning of retirement

Real Rate of Return:
BGN MODE
FV = 0
N = 23
I/Y = 3.43%
PMT = $63,398
PV = ? = $1,031.583.76 = $1,031,578???
16. Victor bought a car for $42,500 as a business investment opportunity. He is allowed to depreciate over 10 years and take it as business tax deduction. At the end of the 10th year he sells this car for $22,000. Compute the cumulative cash benefit after sale on this transaction. Assume that Victor can earn 5% after tax returns and is in 33% tax bracket. Tax rate for Victor on gain is 15%.
$14,340
Step 1: Compute the cumulative tax benefit of depreciation for 10 years
Yearly Deductible Depreciation = $42,500 ÷ 10 = $4,250
Yearly Tax Benefit = $4,250 x 33% = $1,402.50
N = 10
I/Y = 5%
PMT = $1,402.50
PV = 0
FV = ? = $17,640.49
Step 2: Compute the tax to be paid after 10 years on gain at the time of sale
Sale Price in the 10th year = $22,000
Depreciated Value of the car in the 6th year =$42,500 – ($4,250 x 10) = $0
Gain = $22,000 - $0 = $22,000
Tax on Gain = $22,000 x 15% = $3,300
Step 3: Compute Net Cash Earned (Step 1 – Step 2)
Cash Inflow = $17,640.49
Cash Outflow = $3,300
$17,640.49 - $3,300 = $14,340.49
Net Cash Earned = $14,340.49 = $14,340


