Digital control

Question 1

Part (a)

Zero-Order Hold  

A ZOH block represents a zero-order hold circuit in a digital feedback control which together with an ideal sampler is used to hold the previously converted signal at a constant discrete value while a new conversion takes place. An ideal sampler can be represented by a sequence of delta functions. The output of the zero-order hold circuit is a sequence of step functions with amplitudes of m(kT) at the instants of sampling. The figure below illustrates the sample-and-hold device and its operation.

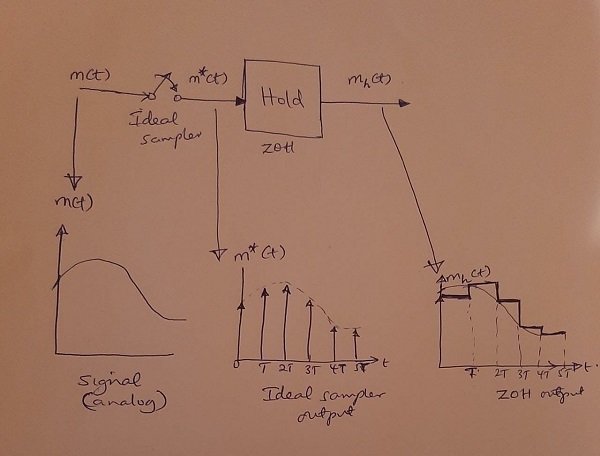
Part (b)

With zero order hold method, the transfer function becomes

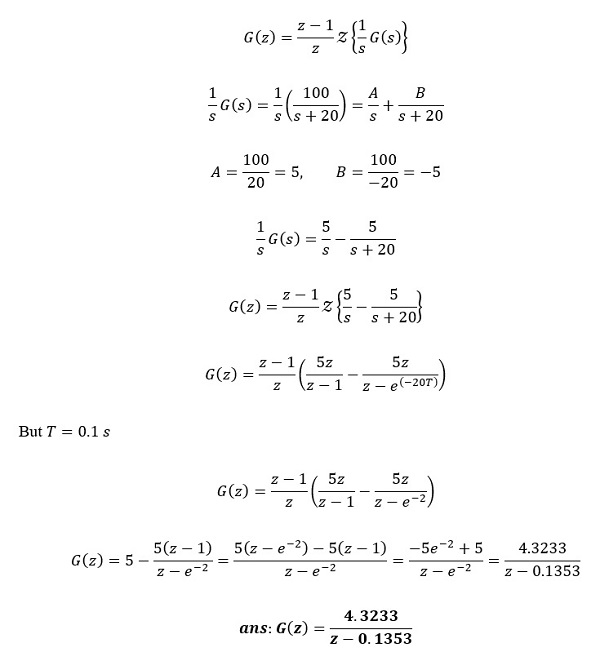
Part (c)

Closed loop transfer function

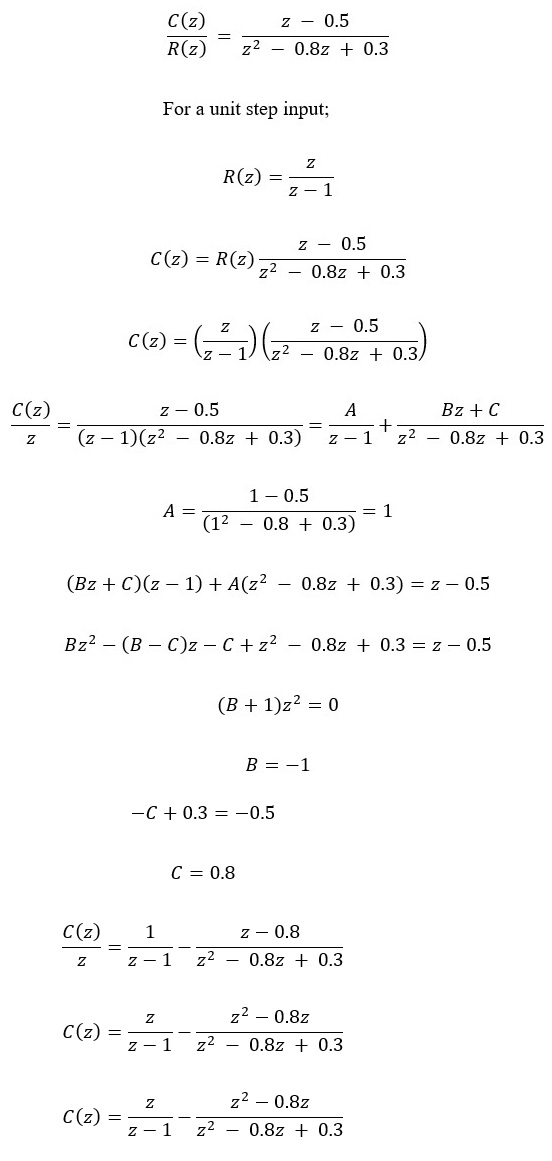
Taking the inverse Z-transform of C(z), we get;

ans:,c₀=-0.0002401,c₁=1,c₂=1.3,c₃=1.24

Question 2

Part (a)

In Backward difference method;

Part (b)

Process, G(z);

ii) To determine the poles of the closed loop transfer function, we factorize the denominator of T(z)

T(z)= (5.6 z - 3.2)/(z² +3.8 z -2.4)= (5.6 z - 3.2)/((z+4.3515)(z-0.5515))

The closed loop poles are:

p₁=-4.3515,p₂=0.5515

Since one of the poles, p₁=-4.3515 lies outside the unit circle, the system is unstable.

Question 4

Part (a)

Advantages of pole assignment for controller design

In pole placement design, all the system poles are placed at the desired locations using state-feedback matrix.

The system poles can be shifted to meet the design requirements and shape the system’s closed loop characteristics.

The closed loop system is stable.

Disadvantages of pole assignment for controller design

Pole placement does not guarantee a robust system.

Design by pole-placement is not insensitive to external disturbance and to variations in the system parameters.

The closed loop poles locations on the complex plain are difficult to determine and requires the establishment of a relationship between dynamic system performance and the system poles.

Part (b)

Let the forward path transfer function be T(z):

Part (c)

Open loop process;

ii) Designing H

Moving the block H inside the feedback loop, we multiply G by 1/H;

The forward path gain is:

Open loop process;

{`
  clear
  clc
  syms z
  H = (3.5*z-2) / (z-1);
  iztrans(H)
  C=(z/(z-1))*((z-0.5)/(z^2-0.8*z+0.3))
  Z=vpa(iztrans(C),3)
  syms n
  Z1 =(-1.0)^n*10.0^(1.0 - 1.0*n)*(- 4.0 - 3.74i)^(n - 1.0)*0.401i - (-1.0)^n*10.0^(1.0 - 1.0*n)*(- 4.0 + 3.74i)^(n - 1.0)*0.401i + 1.0
  Z0=vpa(subs(Z1,n,3),4)
  s=tf("s");
  G1=100/(s+20)
  Gz=c2d(G1,0.1,"zoh")
  z=tf("z");
  G=1.6/(z-0.8)
  D=(3.5*z-2)/(z-1)
  T=feedback(D*G,1)
  isstable(T)
  p=pole(T)`}
  

References

Kuo, B. C. (2017). Digital control systems (pp. 120–125). Oxford University Press.

Nise, N. S. (2019). Nise’s Control systems engineering. John Wiley & Sons.

Ogata, K., & Pearson. (2016). Modern control engineering (pp. 86–107). Pearson.