Differentiation Assignment Help

Differentiation Introduction

Differentiation is all about finding rates of change of one quantity compared to another. We need differentiation when the rate of change is not constant. The slope of a curve at a point tells us the rate of change of the quantity at that point. The process of finding a derivative is called differentiation.

Rules for Differentiation

The Constant Rule

If y = c where c is a constant,

dy/dx = 0

e.g. y = 10 then

dy/dx = 0

dy/dx = 0

The Linear Function Rule

If y = a + bx

dy/dx = b

e.g. y = 10 + 6x then

dy/dx = 6

The Power Function Rule

If y = axⁿ, a & n are constants

dy/dx = n . a . x^n-1

i) y = 4x =>

dy/dx = 4 x ⁰ = 4

ii) y = 4x² =>

dy/dx = 8 x

iii) y = 4x³ =>

dy/dx = 12 x²

iv) y = 4x-2 =>

dy/dx = - 8 x ^{- 3}

The Sum-Difference Rule

If y = f(x) ± g(x)

---

Differentiation Assignment Help By Online Tutoring and Guide Sessions at AssignmentHelp.Net

---

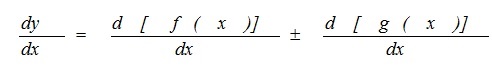
If y is the sum/difference of two or more functions of x: differentiate the 2 (or more) terms separately, then add/subtract.

(i) y = 2x² + 3x then

dy/dx = 4 x + 3

(ii) y = 4x2 - x3 - 4x then

dy/dx = 8 x - 3 x ² - 4

(iii) y = 5x + 4 then

dy/dx = 5

The Product Rule

If y = u.v where u and v are functions of x Then

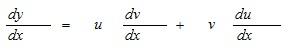
i) y = (x+2)(ax²+bx)

dy/dx = (x + 2)(2 ax + b)+(ax ² + bx)

ii) y = (4x³-3x+2)(2x²+4x)

dy/dx = (4 x ³ - 3x +2)(2x² + 4x)

dy/dx =(4x³ - 3 x + 2)(4 x + 4) + (2 x ² + 4 x)(12 x² - 3)

The Quotient Rule

If y = u/v where u and v are functions of x

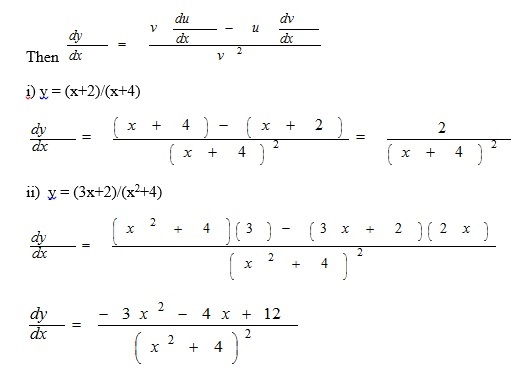
The Chain Rule

If y is a function of v, and v is a function of x, then y is a function of x and

dy/dx = dy/dv . dv/dx

i) y = (ax² + bx)

let v = (ax² + bx), so y = v

dy/dx = 1/2 (ax ² + bx )^-1/2 . (2 ax + b)

ii) y = (4x³ + 3x 7 )⁴

let v = (4x³ + 3x 7 ), so y = v⁴

dy/dx = 4(4x³ + 3x - 7)³ . (12 x² + 3)

The Inverse Function Rule

If x = f(y) then dy/dx = 1/ dx/dy

The derivative of the inverse of the function x = f(y), is the inverse of the derivative of the function

(i) x = 3y² then

dy/dx = 6 y so dy/dx = 1/6y

(ii) y = 4x³ then

dy/dx = 12 x² so dx/dy = 1/12 x²

Rule 9: Differentiating Natural Logs

if y = loge x = ln x =>

dy/dx = 1/x

NOTE: the derivative of a natural log function does not depend on the co-efficient of x

Thus, if y = ln mx => dy/dx = 1/x

Proof

if y = ln mx m>0

Rules of Logs => y = ln m+ ln x

Differentiating (Sum-Difference rule)

dy/dx= 0 + 1/x = 1/x

Example:

Find the equation of the normal to the curve y = 3 x - x at the point where x = 4.

Solution:

The curve can be written as y = 3x^1/2 - x

Therefore, dy/dx = 3/2 x^-1/2 - 1

When x = 4, y = 34 - 4 = 2

and dy/dx = 3/2*4^-1/2 -1 = 3/2*1/2*-1 = -1/4

So the gradient of the normal is m = -1/ -1/4 = 4 .

To find the equation of the tangent:

y = mx + c => y = 4x + c

Substitute x = 4, y = 2: 2 = 4(4) + c i.e. c = -14.

So equation is y = 4x 14.

Important functions for differentiation:

Exponential and logarithmic functions:

d/dx e^x = e^x.

d/dx a^x = In(a)a^x.

d/dx In(x) = 1/x, x >0.

d/dx log_a(x) = 1/x In(a).

Trigonometric functions:

d/dx sin(x) = cos(x).

d/dx cos(x) = -sin(x).

d/dx tan(x) = sec² = 1/cos²(x) = 1 + tan²(x).

Inverse trigonometric functions:

d/dx arcsin(x) = 1/1-x², -1 < x < 1.

d/dx arccos(x) = - 1/1-x², -1 < x < 1.

d/dx arctan(x) = 1/1 + x²