Differential Equations
Question 4
Part (a)
The information given implies that:
dx/dt∝-y,x decreases at a rate proportional to y
dy/dt∝x,y increases at a rate proportional to x
The constant of proportionality is the same,k for the two equations (Balamuralitharan, 2018): Therefore the system of differential equations are (Bird, 2017):
x'=dx/dt=-ky
y'=dy/dt=kx
In matrix form:

Using MATLAB we get:
Q4a:Obtaining eigenvalues and eigenvectors
syms k v1 v2
A=[0 -k; k 0];
Eigenvalues_Q4a=eig(A) %finding eigenvalues
[Eigenvectors_Q4a,DiagMat]=eig(A) %finding eigenvectors
Eigenvalues_Q4a =
-k*1i
k*1i
Eigenvectors_Q4a =
[ -1i, 1i]
[ 1, 1]
DiagMat =
[ -k*1i, 0]
[ 0, k*1i]
Q4b: Solving the system of ODE
syms x(t) y(t)
%defining the odes
ode1=diff(x,t)==-4*y;
ode2=diff(y,t)==4*x;
odee=[ode1,ode2];
%defining the initial conditions
cond1=x(0)==1;
cond2=y(0)==0;
cond=[cond1,cond2];
%solving the ODEs using dsolve()
soln=dsolve(odee,cond);
x=soln.x;
y=soln.y;
% plotting x(t) and y(t)
t1=0:0.001:5;
figure(1)
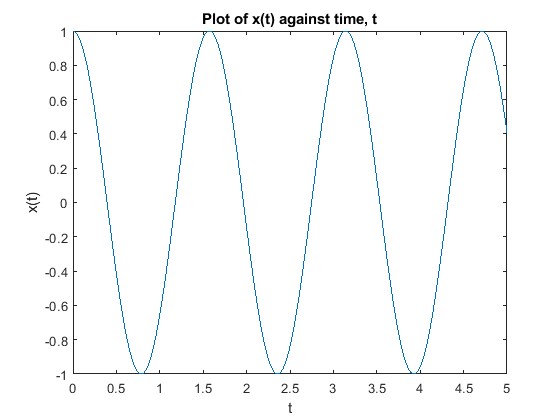
plot(t1,subs(x,t,t1))
xlabel("t")
ylabel("x(t)")
title("Plot of x(t) against time, t")
figure(2)
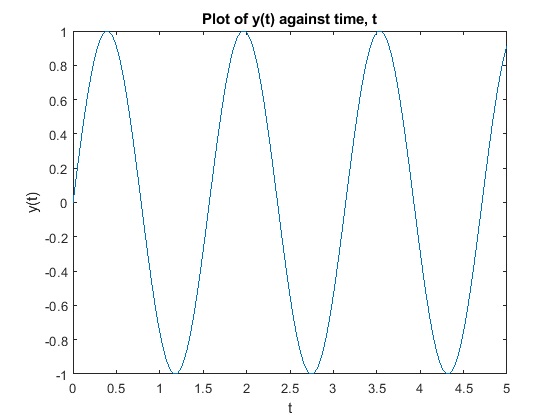
plot(t1,subs(y,t,t1))
xlabel("t")
ylabel("y(t)")
title("Plot of y(t) against time, t")
Question 1
Part a:
Let: (Shiwnarain, 2017)
x1 (t)be the number of larvae at time t
x2 (t) be the number of polliwogs at time t
x3 (t) be the number of catigorgons at time t
x4 (t) be the number of demidogs at time t

MATLAB code and graphs (Magrab et al., 2010)
Q1a: System of ODEs
syms x1(t) x2(t) x3(t) x4(t)
%defining the differential equations
% x1---larvae
% x2---polliwogs
% x3---catigorgons
% x4---demidogs
eqn1=diff(x1,t)==-1/30*x1+5/2*x4;
eqn2=diff(x2,t)==1/30*x1-1/3*x2;
eqn3=diff(x3,t)==1/3*x2-1/2*x3;
eqn4=diff(x4,t)==1/2*x3-1/365*x4;
odee1=[eqn1,eqn2,eqn3,eqn4];
%defining the initial conditions
condi1=x1(0)==20;
condi2=x2(0)==5;
condi3=x3(0)==1;
condi4=x4(0)==0;
condi=[condi1,condi2,condi3,condi4];
% solving the ODEs
soln1=dsolve(odee1,condi);
% obtaining the values of x1, x2, x3 and x4 from the solution
x1=vpa(soln1.x1,3);
x2=vpa(soln1.x2,3);
x3=vpa(soln1.x3,3);
x4=vpa(soln1.x4,3);
% plotting x4---demidogs against time
t2=0:1:400;
figure (3)
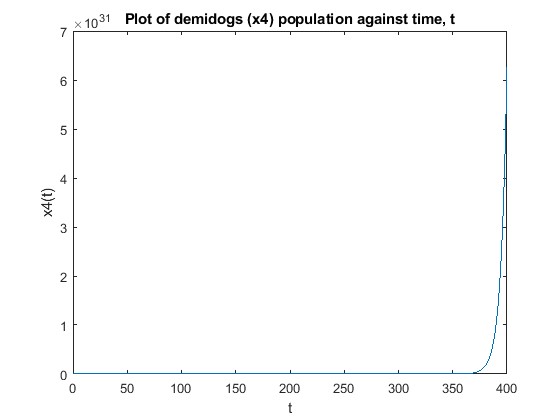
plot(t2,subs(x4,t,t2))
xlabel("t")
ylabel("x4(t)")
title("Plot of demidogs (x4) population against time, t")
disp("The number of demidogs after 7 days")
Demidogs_7=uint64(abs(subs(x1,t,7)))
disp("The number of demidogs after 30 days")
Demidogs_30=uint64(abs(subs(x1,t,30)))
disp("The number of demidogs after 365 days")
Demidogs_365=uint64(abs(subs(x1,t,365)))
Warning: Imaginary parts of complex X and/or Y arguments ignored
The number of demidogs after 7 days
Demidogs_7 =
uint64
70
The number of demidogs after 30 days
Demidogs_30 =
uint64
4970
The number of demidogs after 365 days
Demidogs_365 =
uint64
18446744073709551615
Part b
The coefficient matrix from part (a) is:
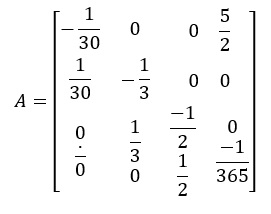
MATLAB Code for eigenvalues of A:
Q1b: Eigenvalues of coefficient matrix from A
A=[-1/30 0 0 5/2; 1/30 -1/3 0 0; 0 1/3 -1/2 0; 0 0 1/2 -1/365];
Eigenvalues_Q1b=eig(A)
Eigenvalues_Q1b =
-0.6273 + 0.0000i
-0.2118 + 0.2775i
-0.2118 - 0.2775i
0.1815 + 0.0000i
References
Balamuralitharan, S. (2018). MATLAB Programming of Nonlinear Equations of Ordinary Differential Equations and Partial Differential Equations. International Journal of Engineering & Technology, 7(4.10), 773. https://doi.org/10.14419/ijet.v7i4.10.26114
Bird, J. (2017). Higher Engineering Mathematics, 8th Ed. Routledge.
Calogero, F. (2013). A linear second-order ODE with only polynomial solutions. Journal of Differential Equations, 255(8), 2130–2135. https://doi.org/10.1016/j.jde.2013.06.007
Dwork, B. (2019). On Systems of Ordinary Differential Equations with Transcendental Parameters. Journal of Differential Equations, 156(1), 18–25. https://doi.org/10.1006/jdeq.1998.3593
King, A. C., & Otto, S. R. (2013). Differential equations : linear, nonlinear, ordinary, partial. Cambridge University Press.
Magrab, E. B., Shapour Azarm, & College, M. (2010). An engineer’s guide to MATLAB. Prentice Hall.
Shiwnarain, M. (2017). Life Cycle Of A Butterfly: Stages Of Life. Science Trends. https://doi.org/10.31988/scitrends.3973
Yamauchi, Y. (2012). Life Span of Positive Solutions for the Cauchy Problem for the Parabolic Equations. International Journal of Differential Equations, 2012, 1–16. https://doi.org/10.1155/2012/417261


