Cive 302 solid mechanics lab report
Data:
|
X (in) |
100lb at P1 (30 in) |
100lb at P2 (60 in) |
100lb at P1/P2 | |
|
d1 |
5 |
-0.011 |
-0.0085 |
-0.0195 |
|
d2 |
25 |
-0.0455 |
-0.04 |
-0.085 |
|
d3 |
45 |
-0.054 |
-0.055 |
-0.1085 |
|
d4 |
65 |
-0.038 |
-0.046 |
-0.084 |
|
d5 |
85 |
-0.0075 |
-0.0095 |
-0.0175 |
Table 1: Experimental displacement readings
|
LC1 |
LC2 |
LC3 | |
|
P1, lbs |
100 |
0 |
100 |
|
P2, lbs |
0 |
100 |
100 |
|
C1 |
-50000 |
-40000 |
-90000 |
|
E, ksi |
10000 | ||
|
I, in^4 |
2.5 | ||
|
L, in |
90 | ||
|
c, in |
1.5 |
Table 2: Given values
Calculations:
|
x (in) |
Moment LC1, lb-in |
Moment LC2, lb-in |
Moment LC3, lb-in |
LC1 disp |
LC2 disp |
LC3 disp |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0.5 |
33.3333 |
16.6667 |
50 |
-0.0010 |
-0.0008 |
-0.0018 |
|
1 |
66.6667 |
33.3333 |
100 |
-0.0020 |
-0.0016 |
-0.0036 |
|
1.5 |
100.0000 |
50.0000 |
150 |
-0.0030 |
-0.0024 |
-0.0054 |
|
2 |
133.3333 |
66.6667 |
200 |
-0.0040 |
-0.0032 |
-0.0072 |
|
2.5 |
166.6667 |
83.3333 |
250 |
-0.0050 |
-0.0040 |
-0.0090 |
|
3 |
200.0000 |
100.0000 |
300 |
-0.0060 |
-0.0048 |
-0.0108 |
|
3.5 |
233.3333 |
116.6667 |
350 |
-0.0070 |
-0.0056 |
-0.0126 |
|
4 |
266.6667 |
133.3333 |
400 |
-0.0080 |
-0.0064 |
-0.0144 |
|
4.5 |
300.0000 |
150.0000 |
450 |
-0.0090 |
-0.0072 |
-0.0161 |
|
5 |
333.3333 |
166.6667 |
500 |
-0.0099 |
-0.0080 |
-0.0179 |
|
5.5 |
366.6667 |
183.3333 |
550 |
-0.0109 |
-0.0088 |
-0.0197 |
|
6 |
400.0000 |
200.0000 |
600 |
-0.0119 |
-0.0096 |
-0.0215 |
|
6.5 |
433.3333 |
216.6667 |
650 |
-0.0129 |
-0.0103 |
-0.0232 |
|
7 |
466.6667 |
233.3333 |
700 |
-0.0138 |
-0.0111 |
-0.0250 |
|
7.5 |
500.0000 |
250.0000 |
750 |
-0.0148 |
-0.0119 |
-0.0267 |
|
8 |
533.3333 |
266.6667 |
800 |
-0.0158 |
-0.0127 |
-0.0285 |
|
8.5 |
566.6667 |
283.3333 |
850 |
-0.0167 |
-0.0135 |
-0.0302 |
|
9 |
600.0000 |
300.0000 |
900 |
-0.0177 |
-0.0142 |
-0.0319 |
|
9.5 |
633.3333 |
316.6667 |
950 |
-0.0186 |
-0.0150 |
-0.0336 |
|
10 |
666.6667 |
333.3333 |
1000 |
-0.0196 |
-0.0158 |
-0.0353 |
|
10.5 |
700.0000 |
350.0000 |
1050 |
-0.0205 |
-0.0165 |
-0.0370 |
|
11 |
733.3333 |
366.6667 |
1100 |
-0.0214 |
-0.0173 |
-0.0387 |
|
11.5 |
766.6667 |
383.3333 |
1150 |
-0.0223 |
-0.0181 |
-0.0404 |
|
12 |
800.0000 |
400.0000 |
1200 |
-0.0232 |
-0.0188 |
-0.0420 |
|
12.5 |
833.3333 |
416.6667 |
1250 |
-0.0241 |
-0.0196 |
-0.0437 |
|
13 |
866.6667 |
433.3333 |
1300 |
-0.0250 |
-0.0203 |
-0.0453 |
|
13.5 |
900.0000 |
450.0000 |
1350 |
-0.0259 |
-0.0211 |
-0.0470 |
|
14 |
933.3333 |
466.6667 |
1400 |
-0.0268 |
-0.0218 |
-0.0486 |
|
14.5 |
966.6667 |
483.3333 |
1450 |
-0.0276 |
-0.0225 |
-0.0502 |
|
15 |
1000.0000 |
500.0000 |
1500 |
-0.0285 |
-0.0233 |
-0.0518 |
|
15.5 |
1033.3333 |
516.6667 |
1550 |
-0.0293 |
-0.0240 |
-0.0533 |
|
16 |
1066.6667 |
533.3333 |
1600 |
-0.0302 |
-0.0247 |
-0.0549 |
|
16.5 |
1100.0000 |
550.0000 |
1650 |
-0.0310 |
-0.0254 |
-0.0564 |
|
17 |
1133.3333 |
566.6667 |
1700 |
-0.0318 |
-0.0261 |
-0.0579 |
|
17.5 |
1166.6667 |
583.3333 |
1750 |
-0.0326 |
-0.0268 |
-0.0594 |
|
18 |
1200.0000 |
600.0000 |
1800 |
-0.0334 |
-0.0275 |
-0.0609 |
|
18.5 |
1233.3333 |
616.6667 |
1850 |
-0.0342 |
-0.0282 |
-0.0624 |
|
19 |
1266.6667 |
633.3333 |
1900 |
-0.0350 |
-0.0289 |
-0.0638 |
|
19.5 |
1300.0000 |
650.0000 |
1950 |
-0.0357 |
-0.0296 |
-0.0653 |
|
20 |
1333.3333 |
666.6667 |
2000 |
-0.0364 |
-0.0302 |
-0.0667 |
|
20.5 |
1366.6667 |
683.3333 |
2050 |
-0.0372 |
-0.0309 |
-0.0681 |
|
21 |
1400.0000 |
700.0000 |
2100 |
-0.0379 |
-0.0315 |
-0.0694 |
|
21.5 |
1433.3333 |
716.6667 |
2150 |
-0.0386 |
-0.0322 |
-0.0708 |
|
22 |
1466.6667 |
733.3333 |
2200 |
-0.0393 |
-0.0328 |
-0.0721 |
|
22.5 |
1500.0000 |
750.0000 |
2250 |
-0.0399 |
-0.0335 |
-0.0734 |
|
23 |
1533.3333 |
766.6667 |
2300 |
-0.0406 |
-0.0341 |
-0.0747 |
|
23.5 |
1566.6667 |
783.3333 |
2350 |
-0.0412 |
-0.0347 |
-0.0759 |
|
24 |
1600.0000 |
800.0000 |
2400 |
-0.0419 |
-0.0353 |
-0.0772 |
|
24.5 |
1633.3333 |
816.6667 |
2450 |
-0.0425 |
-0.0359 |
-0.0784 |
|
25 |
1666.6667 |
833.3333 |
2500 |
-0.0431 |
-0.0365 |
-0.0796 |
|
25.5 |
1700.0000 |
850.0000 |
2550 |
-0.0436 |
-0.0371 |
-0.0807 |
|
26 |
1733.3333 |
866.6667 |
2600 |
-0.0442 |
-0.0377 |
-0.0819 |
|
26.5 |
1766.6667 |
883.3333 |
2650 |
-0.0447 |
-0.0383 |
-0.0830 |
|
27 |
1800.0000 |
900.0000 |
2700 |
-0.0453 |
-0.0388 |
-0.0841 |
|
27.5 |
1833.3333 |
916.6667 |
2750 |
-0.0458 |
-0.0394 |
-0.0851 |
|
28 |
1866.6667 |
933.3333 |
2800 |
-0.0462 |
-0.0399 |
-0.0862 |
|
28.5 |
1900.0000 |
950.0000 |
2850 |
-0.0467 |
-0.0405 |
-0.0872 |
|
29 |
1933.3333 |
966.6667 |
2900 |
-0.0472 |
-0.0410 |
-0.0881 |
|
29.5 |
1966.6667 |
983.3333 |
2950 |
-0.0476 |
-0.0415 |
-0.0891 |
|
30 |
2000.0000 |
1000.0000 |
3000 |
-0.0480 |
-0.0420 |
-0.0900 |
|
30.5 |
1983.3333 |
1016.6667 |
3000 |
-0.0484 |
-0.0425 |
-0.0909 |
|
31 |
1966.6667 |
1033.3333 |
3000 |
-0.0488 |
-0.0430 |
-0.0917 |
|
31.5 |
1950.0000 |
1050.0000 |
3000 |
-0.0491 |
-0.0435 |
-0.0926 |
|
32 |
1933.3333 |
1066.6667 |
3000 |
-0.0494 |
-0.0439 |
-0.0934 |
|
32.5 |
1916.6667 |
1083.3333 |
3000 |
-0.0498 |
-0.0444 |
-0.0941 |
|
33 |
1900.0000 |
1100.0000 |
3000 |
-0.0500 |
-0.0448 |
-0.0949 |
|
33.5 |
1883.3333 |
1116.6667 |
3000 |
-0.0503 |
-0.0452 |
-0.0956 |
|
34 |
1866.6667 |
1133.3333 |
3000 |
-0.0506 |
-0.0457 |
-0.0962 |
|
34.5 |
1850.0000 |
1150.0000 |
3000 |
-0.0508 |
-0.0461 |
-0.0969 |
|
35 |
1833.3333 |
1166.6667 |
3000 |
-0.0510 |
-0.0465 |
-0.0975 |
|
35.5 |
1816.6667 |
1183.3333 |
3000 |
-0.0512 |
-0.0469 |
-0.0981 |
|
36 |
1800.0000 |
1200.0000 |
3000 |
-0.0514 |
-0.0472 |
-0.0986 |
|
36.5 |
1783.3333 |
1216.6667 |
3000 |
-0.0516 |
-0.0476 |
-0.0992 |
|
37 |
1766.6667 |
1233.3333 |
3000 |
-0.0517 |
-0.0479 |
-0.0997 |
|
37.5 |
1750.0000 |
1250.0000 |
3000 |
-0.0518 |
-0.0483 |
-0.1001 |
|
38 |
1733.3333 |
1266.6667 |
3000 |
-0.0520 |
-0.0486 |
-0.1006 |
|
38.5 |
1716.6667 |
1283.3333 |
3000 |
-0.0520 |
-0.0489 |
-0.1010 |
|
39 |
1700.0000 |
1300.0000 |
3000 |
-0.0521 |
-0.0492 |
-0.1013 |
|
39.5 |
1683.3333 |
1316.6667 |
3000 |
-0.0522 |
-0.0495 |
-0.1017 |
|
40 |
1666.6667 |
1333.3333 |
3000 |
-0.0522 |
-0.0498 |
-0.1020 |
|
40.5 |
1650.0000 |
1350.0000 |
3000 |
-0.0522 |
-0.0500 |
-0.1023 |
|
41 |
1633.3333 |
1366.6667 |
3000 |
-0.0523 |
-0.0503 |
-0.1025 |
|
41.5 |
1616.6667 |
1383.3333 |
3000 |
-0.0522 |
-0.0505 |
-0.1028 |
|
42 |
1600.0000 |
1400.0000 |
3000 |
-0.0522 |
-0.0507 |
-0.1030 |
|
42.5 |
1583.3333 |
1416.6667 |
3000 |
-0.0522 |
-0.0509 |
-0.1031 |
|
43 |
1566.6667 |
1433.3333 |
3000 |
-0.0521 |
-0.0511 |
-0.1033 |
|
43.5 |
1550.0000 |
1450.0000 |
3000 |
-0.0521 |
-0.0513 |
-0.1034 |
|
44 |
1533.3333 |
1466.6667 |
3000 |
-0.0520 |
-0.0515 |
-0.1034 |
|
44.5 |
1516.6667 |
1483.3333 |
3000 |
-0.0519 |
-0.0516 |
-0.1035 |
|
45 |
1500.0000 |
1500.0000 |
3000 |
-0.0518 |
-0.0518 |
-0.1035 |
|
45.5 |
1483.3333 |
1516.6667 |
3000 |
-0.0516 |
-0.0519 |
-0.1035 |
|
46 |
1466.6667 |
1533.3333 |
3000 |
-0.0515 |
-0.0520 |
-0.1034 |
|
46.5 |
1450.0000 |
1550.0000 |
3000 |
-0.0513 |
-0.0521 |
-0.1034 |
|
47 |
1433.3333 |
1566.6667 |
3000 |
-0.0511 |
-0.0521 |
-0.1033 |
|
47.5 |
1416.6667 |
1583.3333 |
3000 |
-0.0509 |
-0.0522 |
-0.1031 |
|
48 |
1400.0000 |
1600.0000 |
3000 |
-0.0507 |
-0.0522 |
-0.1030 |
|
48.5 |
1383.3333 |
1616.6667 |
3000 |
-0.0505 |
-0.0522 |
-0.1028 |
|
49 |
1366.6667 |
1633.3333 |
3000 |
-0.0503 |
-0.0523 |
-0.1025 |
|
49.5 |
1350.0000 |
1650.0000 |
3000 |
-0.0500 |
-0.0522 |
-0.1023 |
|
50 |
1333.3333 |
1666.6667 |
3000 |
-0.0498 |
-0.0522 |
-0.1020 |
|
50.5 |
1316.6667 |
1683.3333 |
3000 |
-0.0495 |
-0.0522 |
-0.1017 |
|
51 |
1300.0000 |
1700.0000 |
3000 |
-0.0492 |
-0.0521 |
-0.1013 |
|
51.5 |
1283.3333 |
1716.6667 |
3000 |
-0.0489 |
-0.0520 |
-0.1010 |
|
52 |
1266.6667 |
1733.3333 |
3000 |
-0.0486 |
-0.0520 |
-0.1006 |
|
52.5 |
1250.0000 |
1750.0000 |
3000 |
-0.0483 |
-0.0518 |
-0.1001 |
|
53 |
1233.3333 |
1766.6667 |
3000 |
-0.0479 |
-0.0517 |
-0.0997 |
|
53.5 |
1216.6667 |
1783.3333 |
3000 |
-0.0476 |
-0.0516 |
-0.0992 |
|
54 |
1200.0000 |
1800.0000 |
3000 |
-0.0472 |
-0.0514 |
-0.0986 |
|
54.5 |
1183.3333 |
1816.6667 |
3000 |
-0.0469 |
-0.0512 |
-0.0981 |
|
55 |
1166.6667 |
1833.3333 |
3000 |
-0.0465 |
-0.0510 |
-0.0975 |
|
55.5 |
1150.0000 |
1850.0000 |
3000 |
-0.0461 |
-0.0508 |
-0.0969 |
|
56 |
1133.3333 |
1866.6667 |
3000 |
-0.0457 |
-0.0506 |
-0.0962 |
|
56.5 |
1116.6667 |
1883.3333 |
3000 |
-0.0452 |
-0.0503 |
-0.0956 |
|
57 |
1100.0000 |
1900.0000 |
3000 |
-0.0448 |
-0.0500 |
-0.0949 |
|
57.5 |
1083.3333 |
1916.6667 |
3000 |
-0.0444 |
-0.0498 |
-0.0941 |
|
58 |
1066.6667 |
1933.3333 |
3000 |
-0.0439 |
-0.0494 |
-0.0934 |
|
58.5 |
1050.0000 |
1950.0000 |
3000 |
-0.0435 |
-0.0491 |
-0.0926 |
|
59 |
1033.3333 |
1966.6667 |
3000 |
-0.0430 |
-0.0488 |
-0.0917 |
|
59.5 |
1016.6667 |
1983.3333 |
3000 |
-0.0425 |
-0.0484 |
-0.0909 |
|
60 |
1000.0000 |
2000.0000 |
3000 |
-0.0420 |
-0.0480 |
-0.0900 |
|
60.5 |
983.3333 |
1966.6667 |
2950 |
-0.0415 |
-0.0476 |
-0.0891 |
|
61 |
966.6667 |
1933.3333 |
2900 |
-0.0410 |
-0.0472 |
-0.0881 |
|
61.5 |
950.0000 |
1900.0000 |
2850 |
-0.0405 |
-0.0467 |
-0.0872 |
|
62 |
933.3333 |
1866.6667 |
2800 |
-0.0399 |
-0.0462 |
-0.0862 |
|
62.5 |
916.6667 |
1833.3333 |
2750 |
-0.0394 |
-0.0458 |
-0.0851 |
|
63 |
900.0000 |
1800.0000 |
2700 |
-0.0388 |
-0.0453 |
-0.0841 |
|
63.5 |
883.3333 |
1766.6667 |
2650 |
-0.0383 |
-0.0447 |
-0.0830 |
|
64 |
866.6667 |
1733.3333 |
2600 |
-0.0377 |
-0.0442 |
-0.0819 |
|
64.5 |
850.0000 |
1700.0000 |
2550 |
-0.0371 |
-0.0436 |
-0.0807 |
|
65 |
833.3333 |
1666.6667 |
2500 |
-0.0365 |
-0.0431 |
-0.0796 |
|
65.5 |
816.6667 |
1633.3333 |
2450 |
-0.0359 |
-0.0425 |
-0.0784 |
|
66 |
800.0000 |
1600.0000 |
2400 |
-0.0353 |
-0.0419 |
-0.0772 |
|
66.5 |
783.3333 |
1566.6667 |
2350 |
-0.0347 |
-0.0412 |
-0.0759 |
|
67 |
766.6667 |
1533.3333 |
2300 |
-0.0341 |
-0.0406 |
-0.0747 |
|
67.5 |
750.0000 |
1500.0000 |
2250 |
-0.0335 |
-0.0399 |
-0.0734 |
|
68 |
733.3333 |
1466.6667 |
2200 |
-0.0328 |
-0.0393 |
-0.0721 |
|
68.5 |
716.6667 |
1433.3333 |
2150 |
-0.0322 |
-0.0386 |
-0.0708 |
|
69 |
700.0000 |
1400.0000 |
2100 |
-0.0315 |
-0.0379 |
-0.0694 |
|
69.5 |
683.3333 |
1366.6667 |
2050 |
-0.0309 |
-0.0372 |
-0.0681 |
|
70 |
666.6667 |
1333.3333 |
2000 |
-0.0302 |
-0.0364 |
-0.0667 |
|
70.5 |
650.0000 |
1300.0000 |
1950 |
-0.0296 |
-0.0357 |
-0.0653 |
|
71 |
633.3333 |
1266.6667 |
1900 |
-0.0289 |
-0.0350 |
-0.0638 |
|
71.5 |
616.6667 |
1233.3333 |
1850 |
-0.0282 |
-0.0342 |
-0.0624 |
|
72 |
600.0000 |
1200.0000 |
1800 |
-0.0275 |
-0.0334 |
-0.0609 |
|
72.5 |
583.3333 |
1166.6667 |
1750 |
-0.0268 |
-0.0326 |
-0.0594 |
|
73 |
566.6667 |
1133.3333 |
1700 |
-0.0261 |
-0.0318 |
-0.0579 |
|
73.5 |
550.0000 |
1100.0000 |
1650 |
-0.0254 |
-0.0310 |
-0.0564 |
|
74 |
533.3333 |
1066.6667 |
1600 |
-0.0247 |
-0.0302 |
-0.0549 |
|
74.5 |
516.6667 |
1033.3333 |
1550 |
-0.0240 |
-0.0293 |
-0.0533 |
|
75 |
500.0000 |
1000.0000 |
1500 |
-0.0233 |
-0.0285 |
-0.0518 |
|
75.5 |
483.3333 |
966.6667 |
1450 |
-0.0225 |
-0.0276 |
-0.0502 |
|
76 |
466.6667 |
933.3333 |
1400 |
-0.0218 |
-0.0268 |
-0.0486 |
|
76.5 |
450.0000 |
900.0000 |
1350 |
-0.0211 |
-0.0259 |
-0.0470 |
|
77 |
433.3333 |
866.6667 |
1300 |
-0.0203 |
-0.0250 |
-0.0453 |
|
77.5 |
416.6667 |
833.3333 |
1250 |
-0.0196 |
-0.0241 |
-0.0437 |
|
78 |
400.0000 |
800.0000 |
1200 |
-0.0188 |
-0.0232 |
-0.0420 |
|
78.5 |
383.3333 |
766.6667 |
1150 |
-0.0181 |
-0.0223 |
-0.0404 |
|
79 |
366.6667 |
733.3333 |
1100 |
-0.0173 |
-0.0214 |
-0.0387 |
|
79.5 |
350.0000 |
700.0000 |
1050 |
-0.0165 |
-0.0205 |
-0.0370 |
|
80 |
333.3333 |
666.6667 |
1000 |
-0.0158 |
-0.0196 |
-0.0353 |
|
80.5 |
316.6667 |
633.3333 |
950 |
-0.0150 |
-0.0186 |
-0.0336 |
|
81 |
300.0000 |
600.0000 |
900 |
-0.0142 |
-0.0177 |
-0.0319 |
|
81.5 |
283.3333 |
566.6667 |
850 |
-0.0135 |
-0.0167 |
-0.0302 |
|
82 |
266.6667 |
533.3333 |
800 |
-0.0127 |
-0.0158 |
-0.0285 |
|
82.5 |
250.0000 |
500.0000 |
750 |
-0.0119 |
-0.0148 |
-0.0267 |
|
83 |
233.3333 |
466.6667 |
700 |
-0.0111 |
-0.0138 |
-0.0250 |
|
83.5 |
216.6667 |
433.3333 |
650 |
-0.0103 |
-0.0129 |
-0.0232 |
|
84 |
200.0000 |
400.0000 |
600 |
-0.0096 |
-0.0119 |
-0.0215 |
|
84.5 |
183.3333 |
366.6667 |
550 |
-0.0088 |
-0.0109 |
-0.0197 |
|
85 |
166.6667 |
333.3333 |
500 |
-0.0080 |
-0.0099 |
-0.0179 |
|
85.5 |
150.0000 |
300.0000 |
450 |
-0.0072 |
-0.0090 |
-0.0161 |
|
86 |
133.3333 |
266.6667 |
400 |
-0.0064 |
-0.0080 |
-0.0144 |
|
86.5 |
116.6667 |
233.3333 |
350 |
-0.0056 |
-0.0070 |
-0.0126 |
|
87 |
100.0000 |
200.0000 |
300 |
-0.0048 |
-0.0060 |
-0.0108 |
|
87.5 |
83.3333 |
166.6667 |
250 |
-0.0040 |
-0.0050 |
-0.0090 |
|
88 |
66.6667 |
133.3333 |
200 |
-0.0032 |
-0.0040 |
-0.0072 |
|
88.5 |
50.0000 |
100.0000 |
150 |
-0.0024 |
-0.0030 |
-0.0054 |
|
89 |
33.3333 |
66.6667 |
100 |
-0.0016 |
-0.0020 |
-0.0036 |
|
89.5 |
16.6667 |
33.3333 |
50 |
-0.0008 |
-0.0010 |
-0.0018 |
|
90 |
0.0000 |
0.0000 |
0 |
0.0000 |
0.0000 |
0.0000 |
Table 3a: Calculated theoretical moment, displacement, and bending stress along the beam length
|
x (in) |
LC1 bending stress (psi) |
LC2 bending stress (psi) |
LC3 bending stress (psi) |
|
0 |
0 |
0 |
0 |
|
0.5 |
20 |
10 |
30 |
|
1 |
40 |
20 |
60 |
|
1.5 |
60 |
30 |
90 |
|
2 |
80 |
40 |
120 |
|
2.5 |
100 |
50 |
150 |
|
3 |
120 |
60 |
180 |
|
3.5 |
140 |
70 |
210 |
|
4 |
160 |
80 |
240 |
|
4.5 |
180 |
90 |
270 |
|
5 |
200 |
100 |
300 |
|
5.5 |
220 |
110 |
330 |
|
6 |
240 |
120 |
360 |
|
6.5 |
260 |
130 |
390 |
|
7 |
280 |
140 |
420 |
|
7.5 |
300 |
150 |
450 |
|
8 |
320 |
160 |
480 |
|
8.5 |
340 |
170 |
510 |
|
9 |
360 |
180 |
540 |
|
9.5 |
380 |
190 |
570 |
|
10 |
400 |
200 |
600 |
|
10.5 |
420 |
210 |
630 |
|
11 |
440 |
220 |
660 |
|
11.5 |
460 |
230 |
690 |
|
12 |
480 |
240 |
720 |
|
12.5 |
500 |
250 |
750 |
|
13 |
520 |
260 |
780 |
|
13.5 |
540 |
270 |
810 |
|
14 |
560 |
280 |
840 |
|
14.5 |
580 |
290 |
870 |
|
15 |
600 |
300 |
900 |
|
15.5 |
620 |
310 |
930 |
|
16 |
640 |
320 |
960 |
|
16.5 |
660 |
330 |
990 |
|
17 |
680 |
340 |
1020 |
|
17.5 |
700 |
350 |
1050 |
|
18 |
720 |
360 |
1080 |
|
18.5 |
740 |
370 |
1110 |
|
19 |
760 |
380 |
1140 |
|
19.5 |
780 |
390 |
1170 |
|
20 |
800 |
400 |
1200 |
|
20.5 |
820 |
410 |
1230 |
|
21 |
840 |
420 |
1260 |
|
21.5 |
860 |
430 |
1290 |
|
22 |
880 |
440 |
1320 |
|
22.5 |
900 |
450 |
1350 |
|
23 |
920 |
460 |
1380 |
|
23.5 |
940 |
470 |
1410 |
|
24 |
960 |
480 |
1440 |
|
24.5 |
980 |
490 |
1470 |
|
25 |
1000 |
500 |
1500 |
|
25.5 |
1020 |
510 |
1530 |
|
26 |
1040 |
520 |
1560 |
|
26.5 |
1060 |
530 |
1590 |
|
27 |
1080 |
540 |
1620 |
|
27.5 |
1100 |
550 |
1650 |
|
28 |
1120 |
560 |
1680 |
|
28.5 |
1140 |
570 |
1710 |
|
29 |
1160 |
580 |
1740 |
|
29.5 |
1180 |
590 |
1770 |
|
30 |
1200 |
600 |
1800 |
|
30.5 |
1190 |
610 |
1800 |
|
31 |
1180 |
620 |
1800 |
|
31.5 |
1170 |
630 |
1800 |
|
32 |
1160 |
640 |
1800 |
|
32.5 |
1150 |
650 |
1800 |
|
33 |
1140 |
660 |
1800 |
|
33.5 |
1130 |
670 |
1800 |
|
34 |
1120 |
680 |
1800 |
|
34.5 |
1110 |
690 |
1800 |
|
35 |
1100 |
700 |
1800 |
|
35.5 |
1090 |
710 |
1800 |
|
36 |
1080 |
720 |
1800 |
|
36.5 |
1070 |
730 |
1800 |
|
37 |
1060 |
740 |
1800 |
|
37.5 |
1050 |
750 |
1800 |
|
38 |
1040 |
760 |
1800 |
|
38.5 |
1030 |
770 |
1800 |
|
39 |
1020 |
780 |
1800 |
|
39.5 |
1010 |
790 |
1800 |
|
40 |
1000 |
800 |
1800 |
|
40.5 |
990 |
810 |
1800 |
|
41 |
980 |
820 |
1800 |
|
41.5 |
970 |
830 |
1800 |
|
42 |
960 |
840 |
1800 |
|
42.5 |
950 |
850 |
1800 |
|
43 |
940 |
860 |
1800 |
|
43.5 |
930 |
870 |
1800 |
|
44 |
920 |
880 |
1800 |
|
44.5 |
910 |
890 |
1800 |
|
45 |
900 |
900 |
1800 |
|
45.5 |
890 |
910 |
1800 |
|
46 |
880 |
920 |
1800 |
|
46.5 |
870 |
930 |
1800 |
|
47 |
860 |
940 |
1800 |
|
47.5 |
850 |
950 |
1800 |
|
48 |
840 |
960 |
1800 |
|
48.5 |
830 |
970 |
1800 |
|
49 |
820 |
980 |
1800 |
|
49.5 |
810 |
990 |
1800 |
|
50 |
800 |
1000 |
1800 |
|
50.5 |
790 |
1010 |
1800 |
|
51 |
780 |
1020 |
1800 |
|
51.5 |
770 |
1030 |
1800 |
|
52 |
760 |
1040 |
1800 |
|
52.5 |
750 |
1050 |
1800 |
|
53 |
740 |
1060 |
1800 |
|
53.5 |
730 |
1070 |
1800 |
|
54 |
720 |
1080 |
1800 |
|
54.5 |
710 |
1090 |
1800 |
|
55 |
700 |
1100 |
1800 |
|
55.5 |
690 |
1110 |
1800 |
|
56 |
680 |
1120 |
1800 |
|
56.5 |
670 |
1130 |
1800 |
|
57 |
660 |
1140 |
1800 |
|
57.5 |
650 |
1150 |
1800 |
|
58 |
640 |
1160 |
1800 |
|
58.5 |
630 |
1170 |
1800 |
|
59 |
620 |
1180 |
1800 |
|
59.5 |
610 |
1190 |
1800 |
|
60 |
600 |
1200 |
1800 |
|
60.5 |
590 |
1180 |
1770 |
|
61 |
580 |
1160 |
1740 |
|
61.5 |
570 |
1140 |
1710 |
|
62 |
560 |
1120 |
1680 |
|
62.5 |
550 |
1100 |
1650 |
|
63 |
540 |
1080 |
1620 |
|
63.5 |
530 |
1060 |
1590 |
|
64 |
520 |
1040 |
1560 |
|
64.5 |
510 |
1020 |
1530 |
|
65 |
500 |
1000 |
1500 |
|
65.5 |
490 |
980 |
1470 |
|
66 |
480 |
960 |
1440 |
|
66.5 |
470 |
940 |
1410 |
|
67 |
460 |
920 |
1380 |
|
67.5 |
450 |
900 |
1350 |
|
68 |
440 |
880 |
1320 |
|
68.5 |
430 |
860 |
1290 |
|
69 |
420 |
840 |
1260 |
|
69.5 |
410 |
820 |
1230 |
|
70 |
400 |
800 |
1200 |
|
70.5 |
390 |
780 |
1170 |
|
71 |
380 |
760 |
1140 |
|
71.5 |
370 |
740 |
1110 |
|
72 |
360 |
720 |
1080 |
|
72.5 |
350 |
700 |
1050 |
|
73 |
340 |
680 |
1020 |
|
73.5 |
330 |
660 |
990 |
|
74 |
320 |
640 |
960 |
|
74.5 |
310 |
620 |
930 |
|
75 |
300 |
600 |
900 |
|
75.5 |
290 |
580 |
870 |
|
76 |
280 |
560 |
840 |
|
76.5 |
270 |
540 |
810 |
|
77 |
260 |
520 |
780 |
|
77.5 |
250 |
500 |
750 |
|
78 |
240 |
480 |
720 |
|
78.5 |
230 |
460 |
690 |
|
79 |
220 |
440 |
660 |
|
79.5 |
210 |
420 |
630 |
|
80 |
200 |
400 |
600 |
|
80.5 |
190 |
380 |
570 |
|
81 |
180 |
360 |
540 |
|
81.5 |
170 |
340 |
510 |
|
82 |
160 |
320 |
480 |
|
82.5 |
150 |
300 |
450 |
|
83 |
140 |
280 |
420 |
|
83.5 |
130 |
260 |
390 |
|
84 |
120 |
240 |
360 |
|
84.5 |
110 |
220 |
330 |
|
85 |
100 |
200 |
300 |
|
85.5 |
90 |
180 |
270 |
|
86 |
80 |
160 |
240 |
|
86.5 |
70 |
140 |
210 |
|
87 |
60 |
120 |
180 |
|
87.5 |
50 |
100 |
150 |
|
88 |
40 |
80 |
120 |
|
88.5 |
30 |
60 |
90 |
|
89 |
20 |
40 |
60 |
|
89.5 |
10 |
20 |
30 |
|
90 |
0 |
0 |
0 |
Table 3b: Continued theoretical calculations
|
X (in) |
100lb at P1 (%) |
100lb at P2 (%) |
100lb at P1/P2 (%) |
|
5 |
10.61 |
6.62 |
8.84 |
|
25 |
5.68 |
9.51 |
6.81 |
|
45 |
4.35 |
6.28 |
4.83 |
|
65 |
4.03 |
6.84 |
5.55 |
|
85 |
5.92 |
4.47 |
2.33 |
Table 4: Error analysis
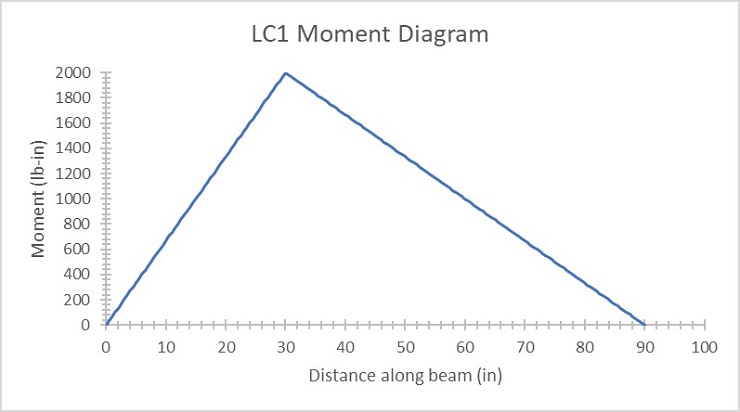
Figure 1: Load case 1 moment diagram
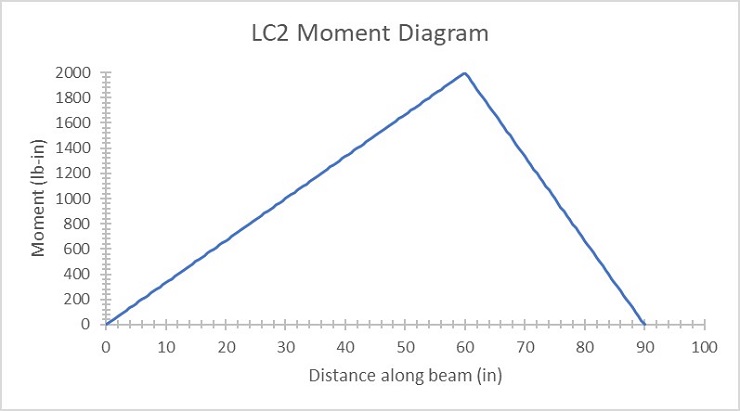
Figure 2: Load case 2 moment diagram
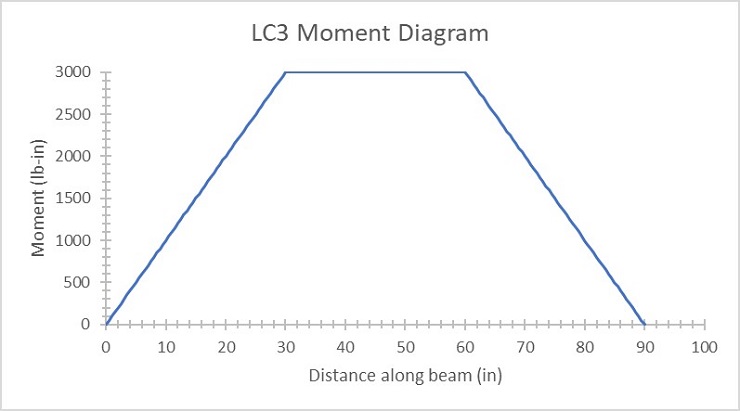
Figure 3: Load case 3 moment diagram
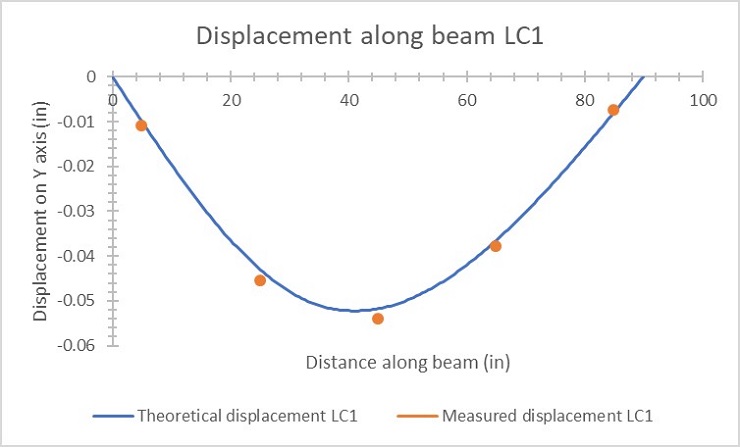
Figure 4: Load case 1 displacement
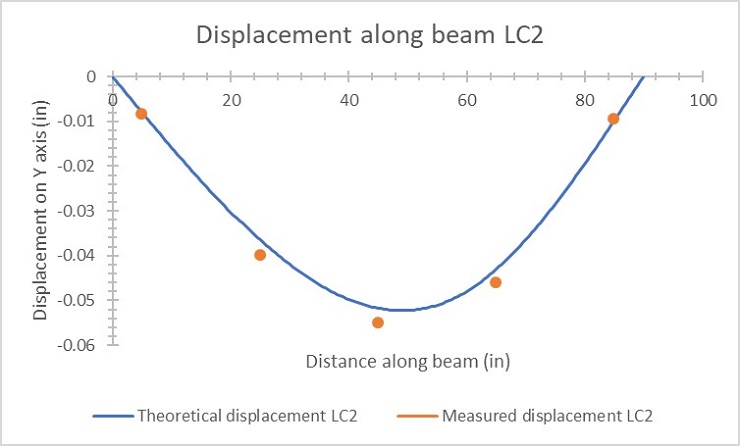
Figure 5: Load case 2 displacement
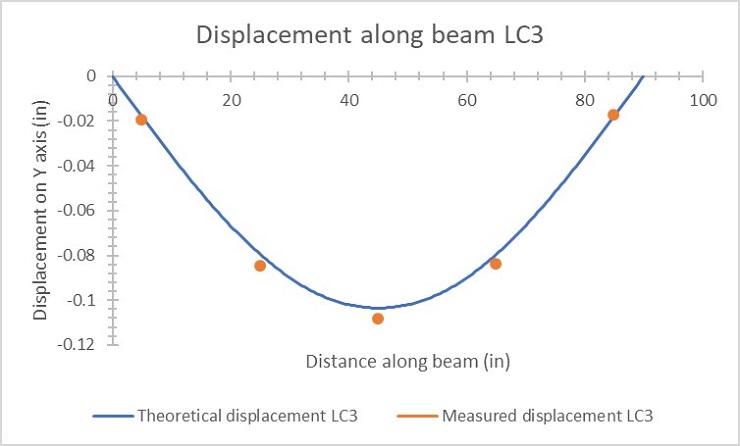
Figure 6: Load case 3 displacement
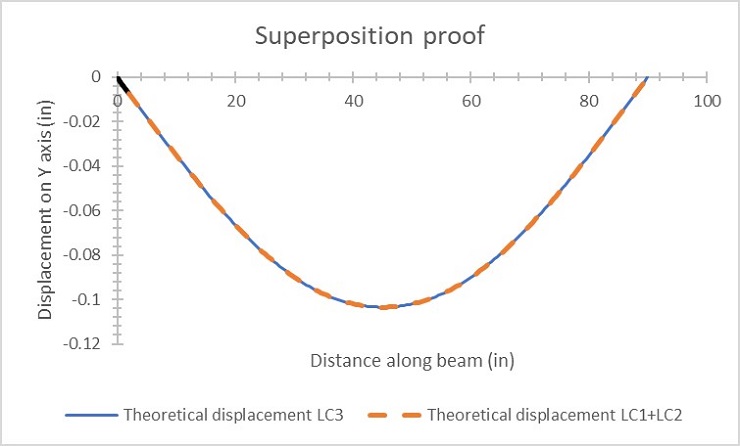
Figure 7: Super position proof
Discussion:
Our theoretical values very closely matched the data gathered during the experiment and were within the margin of error that comes from the theoretical calculations not factoring in the deformation caused by shear which was included in the measurements by the dial indicators. The differences between the calculated theoretical displacement was only off by a few thousandths of an inch at any given point where a dial indicator was located, which is to be expected. The displacement of the beam in the vertical direction is mostly caused by flexural deformation, but shear deformation factors into that as well, albeit a very small amount. This is why the displacement measured by the dial indicator is slightly larger than the values that were calculated. This accounts for most of the error found between the two values. Aside from this error, the experimental and theoretical data line up very closely and follow nearly identical trends when graphed against each other, which can be seen in figures 4-6. Another source of error is the high likelihood that the dial indicators were not perfectly perpendicular to the beam when placed. Once zeroed on the beam, they measure the distance changed on only one axis which would be the vertical axis in this case. If they were not perfectly perpendicular, they would be measuring the hypotenuse of a triangle rather than the vertical distance traveled. All of the length measurements and positioning of the loads as well as dial indicators were placed using a tape measure, which adds yet another source of error. During the experiment, point load 2 shifted slightly between runs two and three as the weights were loaded and unloaded. The weights used not all being exactly 20 pounds may also add more error to the calculations.
Comparing load cases one and two, they display essentially equal and opposite deformation reactions in the beam. To prove the theory of superposition, the deformation reactions from case one and two were added together and should be equal to case three since case three was the loads from cases one and two applied at the same time. This is proven to be true as evidenced by the graph in Figure 7 where the sum of cases one and two overlap the line of case three. The moment diagrams for all three cases are also related and the visual representations make sense since the internal moment should peak where the single loads are applied and when both loads are applied in case three, the moment between the loads should stay constant like it does.


