Welfare Economics Assignment Help
What is welfare?
Economic welfare is the level of satisfaction, prosperity, and standard of living enjoyed by the participants of an economic system. In Economics, the welfare of an individual provides information about the level of utility achieved by that individual from consumption of goods and services.
What is welfare economics?
According to Alfred Marshall, “Economics is the study of mankind in the ordinary business of life”. Economics is a social science as it deals with the behavior of people in a society. Alfred Marshall shifted the focus of economics as a study of wealth to economics as a study of the welfare of the society, thus laying the foundations of welfare economics.
Welfare economics is a specific branch of economics that uses the techniques of microeconomics to study how the distribution of income and other resources affect the economic well-being (or welfare) of the people in an economy.
It studies about the efficient allocation of resources and how this optimal allocation affects the welfare of the people in an economy. In other words, it focuses on how resources are distributed in an economy and how such distribution of resources affects the overall welfare of the economy.
In order to understand the fundamental theorems of welfare economics, it is essential to have good basic understanding of general equilibrium theory. Discussed below is a brief introduction to the concept of general equilibrium in order to comprehend welfare theorems.
Basics of General Equilibrium Theory
Markets of all commodities and factors (input) are interconnected. Prices in all the markets are determined simultaneously. When markets are linked with each other, then a change in the supply or demand condition in one market has an effect on the price and output of the secondary market.
Welfare Economics Assignment Help By Online Tutoring and Guided Sessions from AssignmentHelp.Net
General equilibrium analysis refers to the study of equilibrium in all markets simultaneously. This analysis studies the interaction between demand and supply in a number of markets to determine the prices of many goods.
General equilibrium is a state in which all markets are in equilibrium at the same time and where each consumer is maximizing satisfaction subject to their budget constraint and producers are maximizing their profits subject to technical constraint or the production function.
As it is difficult to study all the markets simultaneously, for the sake of analysis we assume a simple economy where there are only two commodities being produced (1and 2), there are only two factors of production (L for labor and K for capital) and there are only two consumers A and B. In theory, this known as 2×2×2 general equilibrium model.
In order to further simplify our analysis, we make following assumptions of 2×2×2 general equilibrium model:
- a) The technology is given. This means in the simple general equilibrium model; the production function remains same throughout the analysis unless stated otherwise.
- b) All factors of productions are fully employed, and all incomes earned by the owners of these factors are fully spent by the i.e. nothing is saved.
- c) The market is assumed to be perfectly competitive in both factors and commodities market.
Thus, in this simple general equilibrium model, equilibrium is achieved when four markets are in equilibrium (two commodity markets and two-factor markets).
We consider a pure exchange economy wherein all agents are consumers and there is no production going on in the economy and all agents trade with their initial endowments (amount of the two goods 1 and 2, the consumer has before he enters the market to trade).
The Edgeworth Box Diagram
It is a graphical tool which can be used to analyze the exchange of two goods between two people. Edgeworth box helps understand the general equilibrium theory by allowing us to depict the endowments and preferences of the two individuals who are trading with each other.
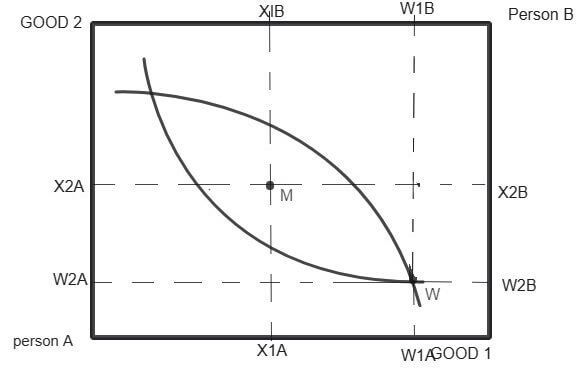
In the above Edgeworth box, the width of the box measures the total amount of good 1 in the economy and length measures the total amount of good 2.
W shows the endowment bundles of the two consumers. Both the consumer can be made better off. Some set of bundles that A prefers intersect with the set of bundles preferred by B.
It is clear from above that it is possible for both consumers to indulge in mutually beneficial trade. Both can be made better off through trade.
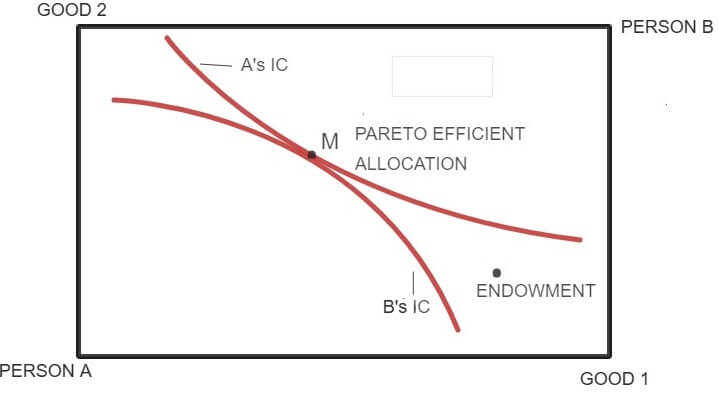
The figure given below depicts the case of Pareto efficiency. Pareto efficiency is an important concept in economics.
An outcome is Pareto optimal if there is no alternative feasible allocation where every individual in the economy is at least as well off and some individuals are strictly well off.
At a Pareto efficient allocation such as point M (figure below), each consumer is said to be on his/her highest possible indifference curve given the indifference curve of another consumer. Since both the consumers A and B have well-behaved preferences, their indifference curves are convex to the origin and are tangent to each other at point M. At point M, it is clear that no consumer can be made better off further, without making another consumer worse off. Thus, a Pareto efficient allocation can be described as an allocation where:
- There is no way in which one consumer can be made better off without making another consumer worse off.
- There is no way in which all consumers can be made better off.
- All the gains which can be utilized through trade have been exhausted. A Pareto efficient allocation is the result of a mutually advantageous trade.
The set of all Pareto efficient allocation points in the Edgeworth box is known as Pareto set or contract curve. At point M, the market is said to have achieved equilibrium (competitive equilibrium).
The condition of Pareto optimality can be defined as a point where slope of the highest possible indifference curve of person A is equal to the slope of highest possible indifference curve of person B i.e.
MRSA = MRSB
According to the concept of Pareto optimality (or say efficiency), any change that makes at least one individual better off without making any other individual worse off is an improvement in social welfare.
Equilibrium in Edgeworth Box
In equilibrium, each person engaged in trade will choose the most preferred bundle available in his budget set. The prices are such that the demand and supply are equal in all the commodity markets.
A competitive general equilibrium is where given the prices (p1, p2) and the allocation (xA, xB), both the consumers A and B maximize their utilities and the market clears i.e. the total demand of goods (1 and 2) is equal to total supply (sum of endowments of the two consumers) of the goods.
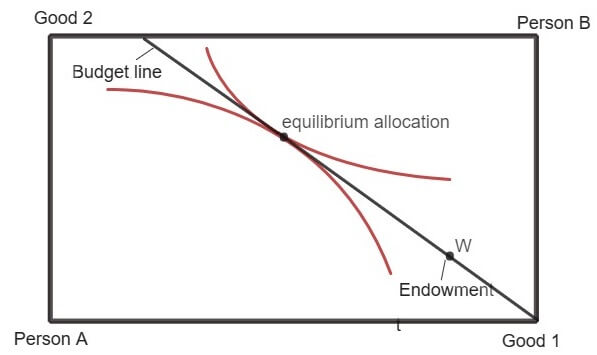
The movement from initial endowment W to a Pareto efficient allocation is achieved by the relative price mechanism. The slope of the line passing through the endowment point represents the price ratio of the commodity 1 and Commodity 2. The equilibrium in a competitive market (for a pure exchange economy) is thus achieved when following condition is satisfied:
MRSA = MRSB = (P1/P2)
At the equilibrium, the set of bundles preferred by A lies above his budget set while the set of bundles preferred by B lies above his budget set (from B’s point of view).
First Theorem of Welfare Economics (Invisible Hand Theorem)
In the entire brief introduction of general equilibrium given above, it has been assumed that the market is competitive. According to the first welfare theorem, the competitive market mechanism will exhaust all the possible gains from trade i.e. it will always lead to Pareto efficient allocation of resources.
Refer to the above diagram showing the equilibrium allocation. At the equilibrium allocation, there is no allocation that both the agents prefer (that I within their budget set) to the equilibrium allocation. Thus, there is no possibility for agents engaging in the trade as there are no gains left to be exhausted. So, we conclude that equilibrium is Pareto efficient.
Implications of First Welfare Theorem
The first welfare theorem provides an analytical confirmation to Adam Smith's hypothesis of the presence of an invisible hand in which competitive markets always lead to efficient allocation of resources without requiring any intervention by the government.
When everybody in the market gets to trade freely given the constraints, then nothing can make everyone better off by taking from one person and giving to another.
A Pareto efficient allocation is not always what is desired by the society. A situation where consumer A holds all the quantities of the good 1 and 2 will be a Pareto efficient distribution but will not be desirable from the society’s point of view. This point will not be probably a fair allocation (from a welfare point of view), although it is efficient. Thus, the first theorem of welfare says nothing about the economic benefits.
Proof of First Theorem of Welfare Economics
The first welfare theorem can be shown numerically. In order to prove this theorem, let us first assume that the equilibrium achieved by the market is not Pareto optimal. This means that there has to be some other feasible allocation which is preferred by both the consumers (A and B). Let that feasible allocation be (z1A, z2A, z1B, z2B) such that
{`
z1A+z1B = w1A+w1B ……1(demand for good 1 = supply of good 1)
z2A+z2B = w2A+w2B ……2 (demand for good 2 = supply of good 2)
(z1A, z2A) >A(x1A, x2A) ……3
(z1B, z2B) >B (x1B, x2B) …….4
`}
Where (x1A, x2A, x1B, x2B) is current equilibrium allocation which is not Pareto efficient (assumed).
At market equilibrium, each individual is assumed to be consuming the best bundle which he/she can afford.
Consider the behavior of consumer A. As (z1A, z2A) is preferred to the best bundle that A chooses, we can say that the preferred bundle (z1A, z2A) is not affordable. This means the bundle (z1A, z2A) costs more than the bundle (x1A, x2A).
Consider the behavior of consumer B. As (z1B, z2B) is preferred to the best bundle that A chooses, we can say that the preferred bundle (z1B, z2B) is not affordable. This means the bundle (z1B, z2B) costs more than the bundle (x1B, x2B).
This result can be shown as:
{`
(P1z1A+p2z2A) >(P1w1A+p2w2A) …….5
(P1z1B+p2z2B) >(P1w1B+p2w2B) ………6
Adding 5 and 6 we get,
(P1z1A+p2z2A) + (P1z1B+p2z2B) > (P1w1A+p2w2A) + (P1w1B+p2w2B)
Or P1(z1A + z1B) + P2(z2A + z2B) > P1(w1A + w1B) + P2(w2A + w2B)
From equations 1 and 2 we get,
P1(w1A + w1B) + P2(w2A + w2B) > P1(w1A + w1B) + P2(w2A + w2B)
`}
The above result is clearly a contradiction as both the sides are actually the same.
We started out by assuming that the market equilibrium was not Pareto optimal. The final contradictory result makes it clear that our assumption was wrong. This follows that all market equilibria are Pareto efficient.
Second Theorem of Welfare Economics
According to the second theorem of welfare economics, on the assumption that every agent in the economy has convex preferences, there will always be prices such that each Pareto efficient allocation is a market equilibrium for a suitable assignment of endowments from all the feasible allocations.
Convex preference is one of the features of well-behaved indifference curves which corresponds to the idea that “averages are preferred to extremes”.
When preferences are not convex, then efficient allocations cannot be achieved by the competitive market. In that case, an allocation may be Pareto efficient, but it will not be a market equilibrium.
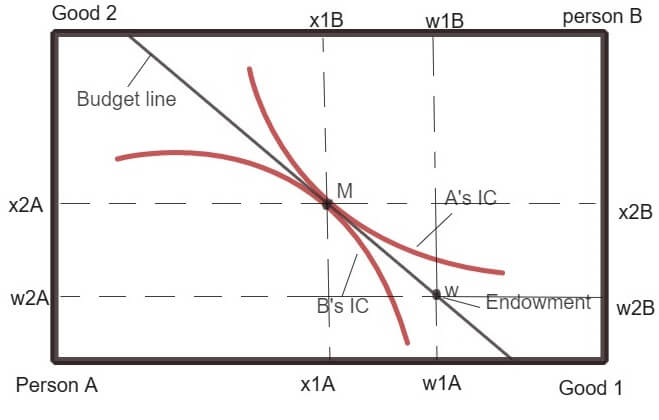
When preferences are convex as shown in the above diagram, then at Pareto optimal allocation the consumption preferred by person A will be disjoint from the bundles which are preferred by person B. As a result, a budget line can be drawn between the two set of preferred bundles.
The slope of the budget line provides the relative price ratio. Any endowment that puts the economic agent on this budget line, results in a market equilibrium that is Pareto efficient.
Implications of Second Welfare Theorem
One of the main issues of economics is improving efficiency with distribution. Second welfare theorem says that the problem of efficiency and distribution must be dealt separately. The competitive market mechanism can be used to achieve a fair distribution of welfare. This can be done by redistributing endowments through lump sum taxes (as they are non-distortionary) or subsidies on endowments i.e. Lump sum transfers of wealth must be used for distributional objectives and then use prices to indicate the relative scarcity of goods.
As long as taxes or subsidies are on the value of the endowments, no efficiency loss occurs as according to the first theorem of welfare economics, no matter how government redistributes endowment, the market equilibrium allocation will always be Pareto efficient.
Online Microeconomics Tutors for General Equilibrium Analysis and Welfare Economics
Need help in understanding microeconomics theory of general equilibrium analysis, Pareto Efficiency, Welfare Economics, Theorems of Welfare Economics and Market Failure? Assignment Help is the best place for you. Assignment Help offers the best microeconomics homework help tutors to help you with online microeconomics homework help for your problem assignments, college homework related to economics term papers, economics research writing work such as economics dissertation writing or help with thesis editing as well as economic analysis through econometrics. So, place your order for Microeconomics homework help now


