Vectors Assignment Help

Introduction to Vectors:

Vectors: Vectors are the quantities which are have both a magnitude and a direction. Vectors only impart magnitude and direction.

Consider the figure below.

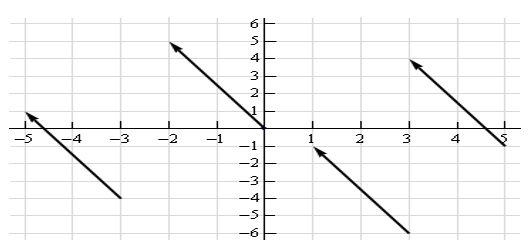
Each line segment in the above figure represents the same vector and each vector starts at specific point and move 2 unit left and 5 units up. The notation for the vector is v^-> =(-2,5)

The vector denotes a magnitude and a direction of a quantity while the point denotes a location in space. A representation of the vector v^-> = (a1,a2) in two dimensional space is any directed line segment, from the point A=(x,y) to the point B= (x+ a1,y+ a2). Likewise a representation of the vector v^-> = (a1,a2,a3) in three dimensional space is any directed line segment, , from the point A=(x,y,z) to the point B= (x + a1,y+ a2+ z+ a3).

The magnitude, or length, of the vector v^-> =(a1,a2,a3) is given by,

v^->=(a²₁ + a²₂ + a²₃ )

Unit vector: Any vector with magnitude of 1, i.e u^-> =1 , is called a unit vector.

Zero Vector: The vector w =(0,0) that we saw in the first example is called a zero vector since its components are all zero. Zero vectors are often denoted by 0 . Be careful to distinguish 0 (the number) from 0 (the vector). The number 0 denotes the origin in space, while the vector 0 denotes a vector that has no magnitude or direction.

Standard Basis Vectors:

The fourth vector from the second example, i =(1,0,0), is called a standard basis vector. In three dimensional space there are three standard basis vectors,

i =(1,0,0)
j =(0,1,0)
k =(0,0,1)

In two dimensional spaces there are two standard basis vectors,

i =(1,0)
j =(0,1)

This standard basis vectors are also unit vectors.

Properties of vector:

If v , w and u are vectors (each with the same number of components) and a and b are two numbers then we have the following properties.

v + ( w) = w + v
u + (v + ( w) ) = (u + ( v) ) + w
v + 0 = v
1v = v
a ( v + w ) = av +aw
(a + b) v = av +bv