Graph Theory Assignment Help
Introduction to graph theory:

A graph consists of a set of dots, called vertices and a set of edges connecting pairs of vertices. A simple graph G is a pair G = (V, E) where V is a nite set, called the vertices of G and E is a subset of P2(V ) (i.e., a set E of two-element subsets of V ), called the edges of G.
Definitions
Vertex: A vertex is a dot in the graph where edges meet. A vertex could represent an intersection of edges.
Edges: Edges connect pairs of vertices.
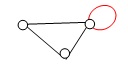
Loop: A loop is a special type of edge that connects a vertex to itself.
Graph Theory Assignment Help By Online Tutoring and Guided Sessions at AssignmentHelp.Net
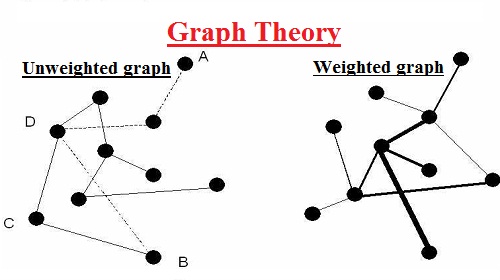
Degree of a vertex: The degree of a vertex is the number of edges meeting at that vertex. It is possible for a vertex to have a degree of zero or larger.

Path: A path is a sequence of vertices using the edges. Usually we are interested in a path between two vertices.
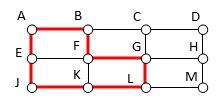
Circuit: A circuit is a path that begins and ends at the same vertex. A circuit starting and ending at vertex A is shown below.
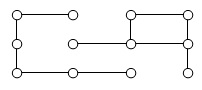
Connected: A graph is connected if there is a path from any vertex to any other vertex. Every graph drawn so far has been connected. The graph below is disconnected; there is no way to get from the vertices on the left to the vertices on the right.
Weights: Depending upon the problem being solved, sometimes weights are assigned to the edges. The weights could represent the distance between two vertices. It is important to note that the distance between vertices in a graph does not necessarily correspond to the weight of an edge.


