Physics Homework Help With Energy Of A Body
Energy Of A Body Is Simultaneous Translation And Rotational Motion
When a body has both translational rotational motion, its total energy can be written as the sum of the two respective kinetic energies. For example, if a body of mass M is rotating about a given axis with an angular speed w and its moment of inertia about the axis is I and simultaneously the axis moves with a linear velocity v, its total energy can be written as
An important case of combined translation and rotation is rolling motion, such as the motion of the wheel shown in figure. The wheel is symmetrical so its centre of mass is at its geometric centre. The rolling motion of this wheel can be analyzed by taking translational and rotational motion separately.
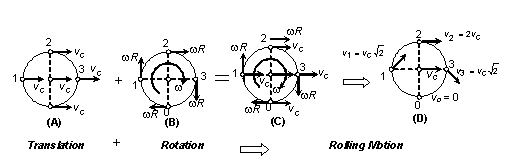
When centre of mass of a wheel moves translational with a speed vcm along with the body in same direction and when it rotates with an angular speed w about its centre, all points on it revolve in different circular paths with the same angular speed w and the points will have linear tangential speed rw if the point is at a distance r from the axis of rotation. If the angular speed of rotation is such that the linear tangential speed of the points on the periphery of the wheel is equal to the translational speed of wheel, then on combining the two motions, the resultant motion is known as pure rolling motion or rolling motion without slipping. This is shown in figure.
In this situation the point on the wheel that contact the surface must be instantaneously at rest so that it does not slip. Hence the velocity rw of the point of contact relative to the centre of mass must have same magnitude but opposite direction as the centre of mass velocity vcm. Thus for pure rolling.
Vcm = rw
The above relation is the condition of pure rolling. Figure shows the velocity of a point on the wheel is the vector sum of the velocity of the centre of mass and the velocity of the point relative to the centre of mass. Thus while point 1, the point of contact, is instantaneously at rest, point 3 at the top of the wheel is moving forward twice as fast as the centre of mass, and point 2 and 4 at the sides have velocities at 45° to the horizontal moving at speed ![]() times the centre of mass.
times the centre of mass.

At any instant we can think of the wheel as rotating about an instantaneous axis of rotation that passes through the point of contact with the ground. The angular velocity w is the same for the axis as for an axis through the centre of mass, an observer at the rim watching the centre of mass spin around him. If we think of motion of rolling wheel in this way, the kinetic energy of the wheel is ![]() where I0 is the moment of inertia of the wheel about an axis through point 1. Using parallel axis theorem I0 = Icm + MR2, where Icm is the moment of inertia of the wheel with respect to an axis through the centre of mass. Thus the kinetic energy in this reference is
where I0 is the moment of inertia of the wheel about an axis through point 1. Using parallel axis theorem I0 = Icm + MR2, where Icm is the moment of inertia of the wheel with respect to an axis through the centre of mass. Thus the kinetic energy in this reference is
![]()
or = ![]()
It is same as that given by equation ![]() . It shows that while solving problems of rolling motion we can solve using both the methods i.e. one by considering the axis of rotation at the centre or in a reference frame attached to the centre of mass of the rolling body and the same problem can also be solved by taking reference frame attached to the instantaneous axis of rotation.
. It shows that while solving problems of rolling motion we can solve using both the methods i.e. one by considering the axis of rotation at the centre or in a reference frame attached to the centre of mass of the rolling body and the same problem can also be solved by taking reference frame attached to the instantaneous axis of rotation.
| Rolling | Sliding | ||
| (i) | Value of friction force | 0 £ f £ fmax | f = fmax |
| (ii) | W.D. by friction force | Wf = 0 | Wf ¹ 0 |
Homework Help For Energy of a body is simultaneous translation and rotational motion
assignmenthelp.net provides best Online Assignment Help service in Physics for all standards. Our Tutor provide their high quality and optimized Tutorial help to fulfill all kind of need of Students.
To submit Energy of a body assignment click here


